はじめに
マウスカーソルの軌跡で線画を描く「お絵かきアプレット」は、Javaのプログラミングを学習するための練習課題としてよく取り上げられます。最低限の機能を実現するには、カーソルの座標を配列に格納し、それを結んで折れ線を描画すればよいので、そんなに難しい話ではありません。しかし、少し気の利いたドローソフトを作ろうとした場合には、描画範囲の拡大縮小(ズーム)や平行移動(パン)の機能が必要になります。このようなズームやパンを行いながら、さらに描画操作を継続できるようにするには、座標変換のための計算が必要になります。
私がネット上で検索した限りでは、ズームとパンという最低限の機能を満たすドローソフトについて、よいサンプルが見つからなかったので、ここでは次のようなアプレットを作成する方法を紹介します。
- マウスの左ドラッグ……カーソルの軌跡で線を描画
- マウスの右ドラッグ……平行移動(パン)
- マウスのホイール……拡大縮小(ズーム)
まずは、完成版アプレットをご覧になってどのようなものなのか動作を確認してみてください。

特別な機能は持ち合わせていないシンプルなアプレットです。このプログラムではJava2DのGraphics2DコンテキストとAffineTransformクラスを活用することで、座標変換に伴う計算を簡単なコードで実現しています。
対象読者
- Javaでドロー系のソフトウェアを作成することに興味のある方
- アフィン変換などCGの基礎知識を学びたい方
必要な環境
J2SE 1.5で動作確認していますが、それ以前のものでもJava2Dが使える環境なら大丈夫と思います。
論理座標とスクリーン座標
ズームもパンも無い簡単なお絵かきアプレットの場合、「マウスカーソルの座標 = 描画するスクリーンの座標」なので、何も難しいことを考える必要はありません。MouseEventクラスのgetPointメソッドでカーソルの座標を取得できるので、その座標をアプレットのpaintメソッドで使用すれば、マウスカーソルの位置に点や線を描画できます。
しかし、ズームとパンを実現する場合は、ユーザーの操作に応じて描画する位置を適切に計算する必要があります。つまり、プログラムの中のデータをアプレットに描画する時に「論理座標」から「スクリーン座標」へ変換する必要があります。
論理座標とは、プログラムの中でデータを保持するのに用いる座標系を指します。一方、スクリーン座標とはアプレットの画面に描画する時に用いる座標系を指します。
座標変換
先ほど述べたように、ズームとパンを行えるアプレットで描画を行う際には、論理座標でプログラム中に保持されているデータをどのようにスクリーン座標に変換するかを考える必要があります(このような座標の変換を「投影」とも呼びます)。
一般に、論理座標(x, y)をスクリーン座標(x', y')に変換するには、次のような変換式で実現できます。
x' = dx + s * x; y' = dy + s * y;
ここでは、sが拡大率を、dxとdyが平行移動量を表します。つまり、ある点の座標値がプログラム内で(x, y)である時、アプレットでは(dx + s * x, dy + s * y)の位置に点を描画すればよいことになります。
一方、マウスカーソルの位置に何かを描画したり、描画された点をクリックして選択するような場合には、逆にマウスカーソルの位置(スクリーン座標)を論理座標での座標値に変換する必要があります(これを「逆変換」と言います)。上記の変換式(式1)を用いて描画している場合、スクリーン座標から論理座標を求める逆変換は次のように表せます。
x = (x' - dx) / s; y = (y' - dy) / s;
ところで、以上で述べたような変換方法は簡単で理解しやすいのですが、ズームイン・アウトの中心は(dx, dy)になってしまいます(sの値をゼロに近づけるとx'=dx、y'=dyとなることから確認できます)。例えば平行移動を行わずに(つまりdx=0、dy=0のときに)、拡大縮小を行うと、図2のように、左上隅を中心とした拡大と縮小が行われます。
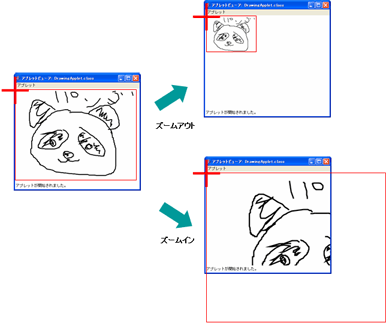
ユーザーの使い勝手を考えると、ズームの中心はスクリーンの中央になるのがよいでしょう。これは、次のような変換式を用いて実現することができます。
x' = cx + s * (x + rx) y' = cy + s * (y + ry)
ここで、cxとcyはスクリーンの中心座標を表し、rx、ryは論理座標での移動量を表します。こうすることで、図3のように拡大縮小の中心がスクリーンの中央と一致します。平行移動を行っても拡大縮小の中心はスクリーンの中央になります(sの値をゼロに近づけるとx'=cx、y'=cyとなることから確認できます)。
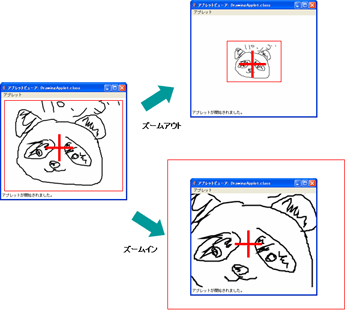
逆変換は、式3をx、yについて解けばよいので、次のようになります。
x = (x' - cx) / s - rx y = (y' - cx) / s - ry
上記の数式は、加減乗除で表現されているものなので、プログラムに実装するのはそれほど難しくありません。
ところで、Java2Dにはアフィン変換を表すAffineTransformというクラスがあり、これを使用すると今まで述べたような数式を用いずに、平行移動とスケール変換を簡単に実現することができます。このAffineTransformは内部的には3x3の行列で表現されており、スクリーン座標から論理座標への逆変換も容易に行えます。
行列を用いたアフィン変換については、以降で説明しますが、理解が難しい場合はAffineTransformクラスの使い方だけを覚えるようにしてもよいでしょう。
アフィン変換とは
アフィン変換とは、図形の平行移動、回転移動、拡大・縮小、せん断の処理を行える、幾何学の変換方式の一種です。2次元図形の場合、次のような3x3の行列演算を用いて表現できます。
[ x'] [ m00 m01 m02 ] [ x ] [ m00 * x + m01 * y + m02 ] [ y'] = [ m10 m11 m12 ] [ y ] = [ m10 * x + m11 * y + m12 ] [ 1 ] [ 0 0 1 ] [ 1 ] [ 1 ]
今回対象としているアプレットでは、論理座標からスクリーン座標への変換に平行移動と拡大・縮小だけを使用するため、このアフィン変換で座標変換を表現できます。例えばs倍に拡大する変換は次の行列演算で表現されます。
[ x'] [ s 0 0 ] [ x ] [ s * x ] [ y'] = [ 0 s 0 ] [ y ] = [ s * y ] [ 1 ] [ 0 0 1 ] [ 1 ] [ 1 ]
また、(dx, dy)の平行移動は次の行列演算で表現されます。
[ x'] [ 1 0 dx ] [ x ] [ x + dx ] [ y'] = [ 0 1 dy ] [ y ] = [ y + dy ] [ 1 ] [ 0 0 1 ] [ 1 ] [ 1 ]
上記から、それぞれスケール変換と平行移動を3x3の行列を用いて表現できることがわかると思いますが、スケール変換と平行移動の両方を行う場合は、行列のかけ算を用いて表現できます。
次の例は、s倍に拡大してから(dx, dy)だけ平行移動する行列演算で式1と同じ変換を行います。
[ x'] [ 1 0 dx ][ s 0 0 ][ x ] [ s 0 dx ][ x ] [ s * x + dx ] [ y'] = [ 0 1 dy ][ 0 s 0 ][ y ] = [ 0 s dy ][ y ] = [ s * y + dy ] [ 1 ] [ 0 0 1 ][ 0 0 1 ][ 1 ] [ 0 0 1 ][ 1 ] [ 1 ]
これらの行列を用いて論理座標からスクリーン座標への変換を行えます。逆行列を用いればスクリーン座標から論理座標を求めることができます。
AffineTransformクラス
平行移動と拡大・縮小は3x3の行列を用いて表現できることを述べましたが、この行列演算を自前でプログラミングするのは手間がかかります。Java2Dでは、これを簡単に扱うAffineTransformという名前のクラスがありますので、これを活用することを考えましょう。
AffineTransformクラスは、内部に3x3の行列を持っていますが、直接行列の各要素を設定せずとも、拡大縮小、平行移動といった変換を施すためのメソッド、translate、scale が準備されています。これを用いることで、自動的に内部の行列が更新されます。生成したAffineTransformオブジェクトを、Graphics2DオブジェクトのsetTransformメソッドの引数に渡せば、後は通常の描画メソッドを実行するだけで、設定したアフィン変換が施された描画が行われます。
例えば次のようなコードで、式3に記したような平行移動と画面中央を基準としたスケール変換を行うAffineTransformオブジェクトを生成できます。
double cx = getWidth() * 0.5; double cy = getHeight() * 0.5; // AffineTransformオブジェクトを生成 AffineTransform affineTransform = new AffineTransform(); affineTransform.translate(cx, cy); // 画面サイズの半分だけ移動 affineTransform.scale(s, s); // s倍のスケール変換 affineTransform.translate(rx, ry); // (rx, ry)だけ平行移動
上のコードでは(rx, ry)の平行移動が行われた後でs倍のスケール変換が行われ、最後に(cx, cy)の平行移動が行われます。コードの中で後に現れる変換がはじめに適用されることに注意しましょう。
上のAffineTransformオブジェクトは論理座標からスクリーン座標を求めるためのものでしたが、スクリーン座標から論理座標に変換するには、inverseTransformメソッドを使用します。このメソッドは次のようにPoint2D型のオブジェクトを2つ引数に取ります。
public Point2D inverseTransform(Point2D ptSrc, Point2D ptDst) throws NoninvertibleTransformException
このメソッドは、指定されたptSrcを逆変換して、その結果をptDstに格納します。また戻り値として変換後の点が返されます。このメソッドの第一引数にマウスカーソルのスクリーン座標を渡すことで、その論理座標を得ることができます。
ソースコード
これまでに説明したAffineTransformクラスを用いたアプレットのコードは次のようになります。コードの後に、ポイントをまとめます。
import java.applet.*; import java.awt.*; import java.awt.event.*; import java.awt.geom.*; import java.util.*; public class DrawingApplet extends Applet implements MouseListener, MouseMotionListener, MouseWheelListener, ComponentListener { // 直前にマウスボタンが押されたポイント(スクリーン座標) private Point2D preMousePoint; private double scale; // 拡大率 private double moveX; // X座標の平行移動量(論理座標) private double moveY; // Y座標の平行移動量(論理座標) private GeneralPath stroke; // 描画中のストローク // アプレットの大きさが変更される前のサイズ private Dimension preSize; private Image bufferImage; // バッファイメージ // バッファイメージのグラフィックコンテキスト private Graphics2D bufferg; // アフィン変換情報 private AffineTransform affineTransform = new AffineTransform(); // ストロークを格納するベクトル private Vector strokes = new Vector(); // ストロークの描画に使用するスタイル final private static BasicStroke strokeStyle = new BasicStroke(3.0f, BasicStroke.CAP_BUTT, BasicStroke.JOIN_MITER); public DrawingApplet() { // 各イベントリスナの登録 addMouseListener(this); addMouseMotionListener(this); addMouseWheelListener(this); addComponentListener(this); } // 初期化処理 public void init() { bufferImage = createImage(getWidth() , getHeight()); bufferg = (Graphics2D)bufferImage.getGraphics(); moveX = 0; moveY = 0; preSize = getSize(); scale = 1.0; setBackground(Color.white); updateAffineTransform(); } // 拡大縮小は画面中央を基準 public void paint(Graphics g) { bufferg.setRenderingHint(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON); // buffergのAffineTransformを初期化 bufferg.setTransform(new AffineTransform()); // バッファのイメージをクリア bufferg.setColor(Color.white); bufferg.fillRect(0, 0, getWidth(), getHeight()); // バッファのAffineTransformを設定する bufferg.setTransform(affineTransform); // ストロークの描画 bufferg.setStroke(strokeStyle); bufferg.setColor(Color.black); for(int i = 0; i < strokes.size(); i++) { bufferg.draw((GeneralPath)strokes.elementAt(i)); } // バッファイメージをアプレット画面に転送 g.drawImage(bufferImage, 0, 0, this); } // 現在のAffineTransformを更新する private void updateAffineTransform() { affineTransform.setToIdentity(); // 初期化 affineTransform.translate(getWidth() * 0.5, getHeight() * 0.5); // 画面中央を基準 affineTransform.scale(scale, scale); // スケール変換 affineTransform.translate(moveX, moveY); // 平行移動 } // スクリーン座標から論理値座標を返す private Point2D.Double getLogicalPositionFromScreenPosition(Point p) throws NoninvertibleTransformException { return (Point2D.Double)affineTransform.inverseTransform( new Point2D.Double(p.x, p.y), null); } public void mousePressed(MouseEvent e) { if((e.getModifiers() & MouseEvent.BUTTON3_MASK) != 0) { // 平行移動の開始 preMousePoint = e.getPoint(); } else { // ストロークの描画開始 try { // 新規ストロークを作成 stroke = new GeneralPath(); // ストロークを保持するベクトルに追加 strokes.add(stroke); // マウスの論理座標を取得 Point2D.Double mousePoint = getLogicalPositionFromScreenPosition(e.getPoint()); // ストロークの初期点を設定 stroke.moveTo((float)mousePoint.x, (float)mousePoint.y ); } catch (Exception ex) { return; } } } public void update(Graphics g) { paint(g); } public void mouseDragged(MouseEvent e) { if((e.getModifiers() & MouseEvent.BUTTON3_MASK) != 0) { // 平行移動量を更新 moveX += (double)(e.getX() - preMousePoint.getX()) / scale; moveY += (double)(e.getY() - preMousePoint.getY()) / scale; preMousePoint = e.getPoint(); updateAffineTransform(); repaint(); } else if((e.getModifiers() & MouseEvent.BUTTON1_MASK) != 0) { // ストロークの更新 try { Point2D.Double mousePoint = getLogicalPositionFromScreenPosition(e.getPoint()); stroke.lineTo((float)mousePoint.x, (float)mousePoint.y ); repaint(); } catch (Exception ex) { return; } } } // マウスホイールによるズームイン・ズームアウト public void mouseWheelMoved(MouseWheelEvent e) { double scale_ = (100.0 - e.getWheelRotation() * 5) / 100.0; scale *= scale_; updateAffineTransform(); repaint(); } // サイズが変更されたときの処理 public void componentResized(ComponentEvent ce) { preSize = getSize(); // 画面の中央の論理座標の更新 moveX = moveX - preSize.width * 0.5 + getWidth() * 0.5; moveY = moveY - preSize.height * 0.5 + getHeight() * 0.5; // バッファイメージの更新 bufferImage = createImage(getWidth() , getHeight()); bufferg = (Graphics2D)bufferImage.getGraphics(); updateAffineTransform(); // 再描画 repaint(); } public void mouseClicked(MouseEvent e) {} public void mouseMoved(MouseEvent e) {} public void mouseReleased(MouseEvent e) {} public void mouseEntered(MouseEvent e) {} public void mouseExited(MouseEvent e) {} public void componentMoved(ComponentEvent ce) {} public void componentShown(ComponentEvent ce) {} public void componentHidden(ComponentEvent ce) {} }
上記のコードの中でポイントとなる部分は次の通りです。
initメソッドの中でダブルバッファ用のイメージオブジェクトを作成し、あらかじめGraphics2Dコンテキストをbuffergに格納しています。- ストロークは
GeneralPathのオブジェクトとしてVectorに格納しています。 - アフィン変換を表すための
AffineTransformオブジェクトをaffineTransformという名前でメンバに持っています。 affineTransformは、ズーム、パンが行われたとき、およびアプレットのサイズが変更されたときにupdateAffineTransformメソッドで再計算しています。- マウスドラッグで平行移動するときは、画面上での移動量とマウスの移動量が一致するように、マウスの移動量を
1/scale倍しています。
おわりに
今回のアプレットは、アンドゥもクリアの機能も備わっていない、非常に簡単なものです。ここで紹介したコードを雛形として、必要な機能を適宜追加していただければと思います。














































