疎行列の計算を実装してグラフ理論をかじってみる

　長いお休みの間コードを触ってないと休み明けのリハビリがしんどいので、それといった目的もなくVisual Studioと戯れておりました。せっかくだから（？）普段めったにやらない分野で遊ぼうと「グラフ理論を行列で学ぶ」ってお題でコードを書いてたんですけど、なんだか面白い結果が出てきちゃったので紹介しておきますね。

　グラフ理論でいうところの「グラフ」とは、折れ線グラフや円グラフのグラフじゃなくて、下図のような頂点（vertex,node）を辺（edge）で繋いだもの。複数の島に橋がかかったような見てくれです。

　このグラフでは辺を矢印で表しています。一方通行の橋というわけで、島0から島1へは渡れるけれど逆行は不可、と。

　例えばTwitterだと各アカウントを頂点（島）、他アカウントのフォローを辺（橋）としたグラフで表現できます。Facebookのアカウントと友達関係も同様ですが、この場合は辺に方向がありません。辺に方向があるグラフを有向グラフ、方向がないのは無向グラフと呼ばれます。TwitterやFacebook、あるいはWebページのリンクなどだと山ほどの島に橋のかかったとてつもない規模のグラフになりますな。

グラフを行列で表現する

　このグラフを行列で表現したのがコチラ。

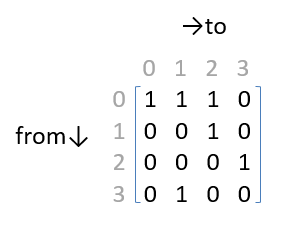
　この行列のi行j列成分は「島iから島jに渡れるか否か」を1／0で表しています。「（橋を介して）島どうしが隣り合っているか否か」を表しているので隣接行列（adjacency matrix）といいます。

　この行列をコードで表現するのはとっても簡単、頂点（島）の数だけの行数／列数で2次元配列：matrix[4][4] を用意するだけ――ですが少なからず不安が残ります。行列の表現に必要な領域が頂点数の二乗なんですよね。この例では頂点数4だからどってことありませんけど、これが1000になったら百万、10000になったら一億個分の領域を食いつぶします。

　この例では成分の総数すなわち頂点数^2=16に対し非0成分の数（橋の数）=6 ですから、行列の60%以上は0で埋まっています。行列から0成分を取り除くとスカスカになる（ほとんどの成分が0である）行列を疎行列（sparse matrix）と称します。疎行列なら0成分が占める領域を省略する（非0成分の領域のみを確保する）ことでメモリの使用量を減らすことができます。

　疎行列をコードで実現すべく、こんなデータ構造を用意しました。

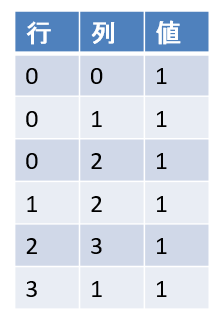
　なんのことはない、行／列／値の組を要素とする配列（vector）です。i行j列の成分を参照する際はこの表を引くことになりますが、表引きの速度を上げるため行・列でソートしておき、二分検索（binary search）することにしましょう。ただし、新たな成分を追加する際vectorの途中に要素を割り込ませるのは時間がかかるので、いったんvectorの末尾に積み上げておいて、複数の要素の挿入が完了した時点でまとめてソートします。

　「行・列indexと値」を要素とするvectorを内包し、やっつけ仕事で実装した疎行列 sparse::matrixを以下に示します。i行j列の成分（値）を返すメンバ関数at()は、i,jの組が表にあるか否かを判定できるようboolを返すことにしました。

list-1　sparse\matrix.h

#ifndef SPARSE_MATRIX_H_
#define SPARSE_MATRIX_H_

#include <vector>     // vector
#include <iterator>   // advance
#include <utility>    // pair
#include <algorithm>  // implace_merge, sort, etc.
#include <cassert>    // assert

template<typename Pair>
struct first_less {
  bool operator()(const Pair& x, const Pair& y) const {
    return x.first < y.first;
  }
};

namespace sparse {

template<typename T>
class matrix {
public:
  using key_type   = std::pair<int,int>;      // 位置(first,second) = (y,x)
  using value_type = std::pair<key_type,T>;   // 行列の[y][x]成分
  using container  = std::vector<value_type>;
  using compare    = first_less<value_type>;
private:
  container dictionary_; // 可変長配列による辞書
  typename container::size_type sorted_size_; // dictionary_の先頭からココまでソート済

public:

  matrix() : sorted_size_(0) {}

  void finalize() {
    // dictionary_を再ソートする
    if ( dictionary_.size() != sorted_size_ ) {
      // dictionary_.begin() から mid まで（前半）はソート済なので
      container::iterator mid = dictionary_.begin();
      std::advance(mid, sorted_size_);
      // mid から　dictionary_.end() まで（後半）をソートし
      std::sort(mid, dictionary_.end(), compare());
      // 前半と後半をマージする
      std::inplace_merge(dictionary_.begin(), mid, dictionary_.end(), compare());
      sorted_size_ = dictionary_.size();
    }
  }

  void clear() {
    // dictionary_を空にする
    sorted_size_ = 0; dictionary_.clear();
  }

  std::size_t size() const { return dictionary_.size(); }

  bool ok() const {
    // dictionary_にrow.colの重複がなければtrueを返す
    // ただし、dictionary_は（finalize()によって）ソート済でなければならない
    return std::adjacent_find(dictionary_.begin(), dictionary_.end()) == dictionary_.end();
  }

  typename container::const_iterator find_at(int row, int col) const {
    // row,col の組を dicrtionary_ から探す
    assert( dictionary_.size() == sorted_size_ );
    value_type tmp(std::make_pair(row,col), T());
    container::const_iterator iter = 
      std::lower_bound(dictionary_.cbegin(), dictionary_.cend(), tmp, compare());
    return ( iter != dictionary_.cend() && iter->first == tmp.first ) 
      ? iter : dictionary_.end();
  }

  void insert(int row, int col, const T& val) {
    // row, col, val の組を dictionary_の末尾に挿入する
    dictionary_.emplace_back(std::make_pair(row,col), val);
  }

  T* at(int row, int col, T* valp) const {
    // rpw,colの組がdictionary_にあるなら対応する値を(*valp)
    // にセットし、valpを返す(なければnullptrを返す)
    container::const_iterator iter = find_at(row, col);
    if ( iter == dictionary_.end() ) return nullptr;
    *valp = iter->second;
    return valp;
  }

  bool at(int row, int col, T& val) const {
    // rpw,colの組がdictionary_にあるなら対応する値をval
    // にセットし、trueを返す（なければfalseを返す）
    return at(row, col, &val) != nullptr;
  }

  bool replace_at(int row, int col, const T& val) {
    // rpw,colの組がdictionary_にあるなら対応する値をval
    // に変更し、を返す（なければfalseを返す）
    container::iterator iter = find_at(row, col);
    bool found = iter != dictionary_.end();
    if ( found ) {
      iter->second = val;
    }
    return found;
  }

  template<typename Function>
  void enumerate(Function fn) const {
    // dictionary_内の各 row,col,val を引数としてfnを呼ぶ
    for ( const value_type& entry : dictionary_ ) {
      fn(entry.first.first, entry.first.second, entry.second);
    }
  }

};

}
#endif

　それとついでに、疎行列どうしの掛け算関数：multiplies()と対角成分を埋めるfill_diagonal()も。

list-2　sparce\multiplies.h

#ifndef SPARSE_MULTIPLIES_H_
#define SPARSE_MULTIPLIES_H_

#include "matrix.h"

namespace sparse {

template<typename T>
matrix<T> multiplies(const matrix<T>& A, const matrix<T>& B, int k, int l, int m) {
  matrix<T> out;
  // out[row, col] = Σ(A[row,i] * B[i,col]
  for ( int row = 0; row < k; ++row ) {
    for ( int col = 0; col < m; ++col ) {
      T sum = T(0);
      T aval;
      T bval;
      for ( int i = 0; i < l; ++i ) {
        aval = T(0); A.at(row, i, aval);
        bval = T(0); B.at(i, col, bval);
        sum += aval * bval;
      }
      if ( sum != T(0) ) {
        out.insert(row, col, sum);
      }
    }
  }
  out.finalize();
  return out;
}

}
#endif

list-3　sparse\fill_diagonal.h

#ifndef SPARSE_FILL_DIAGONAL_H_
#define SPARSE_FILL_DIAGONAL_H_

#include "matrix.h"
namespace sparse {

template<typename T>
void fill_diagonal(matrix<T>& mtx, int n, const T& val) {
  // (0,0), (1,1) ... (n-1,n-1) を val で埋める
  for ( int i = 0; i < n; ++i ) {
    mtx.insert(i, i, val);
  }
  mtx.finalize();
}

}
#endif