はじめに
実験結果をグラフに表示する時、測定点をプロットしてから、測定点に近い直線や二次曲線などを描くことがあります。ここでは、これを自動的に行うプログラムを紹介します。この作業は「曲線の当てはめ」と呼ばれ、「最小二乗法」が用いられますが、対数目盛を含む各種グラフの座標上で回帰直線を求め、指数関数、対数関数、冪(べき)関数にも対応できるよう工夫しました。
- 完成版アプレットを見る
対象読者
最小二乗法に興味を持ち、実験結果をまとめるのに、自分で作ったプログラムを応用したい人。
必要な環境
J2SE 5.0を使っていますが、それより古いバージョンでも大丈夫です。
最小二乗法による曲線の当てはめ
最小二乗法による曲線の当てはめは、Least Squares Fittingと呼ばれ、測定データとの誤差の二乗の和が最小になるような、与えられた形式の式(実験式)を求めることをいいます。「補間」が測定データを絶対視し、それらを必ず通る曲線を描き、中間の値を推定したのに対し、「当てはめ」は、測定データからの誤差を最小にする式を求めます。
線形多項式への当てはめが一般的だが、理工学分野では、あまり意味がない
一番単純な当てはめは直線(一次式)で近似するもので、その直線は「回帰直線」と呼ばれ、統計で多く用いられます。二次式や三次式、またはそれ以上の多項式を当てはめる場合もあり、これは多元連立方程式を解いて求めます。これらは、線形代数学の範囲のため、「線形最小二乗法」とも呼ばれます。しかし、実際には、測定データは理論的に平方根、指数、冪(べき)などの形をとるべきものが多く、それらを無理に線形多項式に当てはめるのは意味がありません。
非線形の式への当てはめは難しい
多くの物理現象は、線形多項式では表現できません。これらに対応した曲線に当てはめるには、「非線形最小二乗法」があり、Gauss-Newton法、Levenberg-Marquardt法などが知られています。しかし、理論が難解で、プログラムも簡単ではありません。
対数目盛を含むグラフ上で回帰直線を求めると、非線形最小二乗法と似た効果がある
対数目盛を含むグラフ上で、従来の線形最小二乗法の最も簡単な例である回帰直線を求め、それを通常の線形グラフに変換すると、いくつかの非線形曲線に対する当てはめが可能になります。詳細については、後述の参考資料を参照して下さい。
下表のように、4種類のグラフを使用すると、一次関数、指数関数、対数関数、冪(べき)関数に対して意味のある当てはめができます。
| グラフの種別 | 回帰直線の式 | 変形結果 | 当てはめ可能な関数 |
| 線形→線形 |  | 一次関数 | |
| 線形→対数 |  |  | 指数関数 |
| 対数→線形 |  | 対数関数 | |
| 対数→対数 |  |  | 冪(べき)関数 |
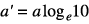 、
、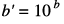
例えば、クーロンの法則は、距離の二乗に反比例した力が働くので、 の冪関数が使えます。共振周波数は、LCの積の平方根に反比例しますので、
の冪関数が使えます。共振周波数は、LCの積の平方根に反比例しますので、 の冪関数になります。また、コンデンサの放電電圧の時間変化は、
の冪関数になります。また、コンデンサの放電電圧の時間変化は、 の指数関数で表現できます。
の指数関数で表現できます。
回帰直線の求め方
線形最小二乗法は、一般に多項式に当てはめます。そして、多元連立方程式を解くのが普通です。数値計算法では、Gaussその他の解法が知られています。しかし、ここでは、回帰直線と呼ばれる最も簡単な1次式への当てはめを使用しますので、特に連立方程式を解くまでもなく、多くの参考資料に示されている下記の公式を利用します。
当てはめたい一次式を とすると、
とすると、
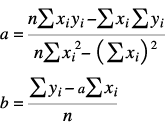
プログラムの説明
各種ボタンの動作
ボタンをクリックすると、regression_flag、final_flagがそれぞれ下表の通り設定され、repaintします。
| ボタン | regression_flag | final_flag | その他 |
| 初期状態 | false | false | data_count=0data_value[i]=0.0 |
| [回帰直線] | true | false | |
| [回帰決定] | false | true | createRegressionValueを呼び出し、回帰直線上の501個の点を、Point2D.Doubleクラスの数値regression_value[i]に変換し、格納します。また、決定時のグラフ種別をselectionに格納します。 |
| [回帰消去] | false | false | |
| [データ消去] | false | false | data_count=0data_value[i]=0.0 |
画面上の位置とグラフ上の数値の換算
このプログラムで重要な役割を演じ、頻繁に用いられているのが、画面上の位置とグラフ上の数値の相互変換です。
下記条件について注意してください。
- 画面上の位置
(x, y)は、(X0, Y0+100*SIZE)を原点とし(X0とY0は、「方眼紙」の左上の座標)、縦軸は上に向かって正符号をとります。 - 回帰直線は、この
xとyに対して算出し、画面に描画します。 - ディスプレイ画面のピクセル位置は、
(X0+x, Y0+100*SIZE-y)となります。 - グラフ上で「100x100」の数値を「500x500」の画面に表示する場合は、
SIZE=5となります。
以下は、xのみについて示していますが、yについても同様です。
| 目盛 | 画面上の位置(position) | 数値(value) |
| 線形 |  |  |
| 対数 |  |  |
| 目盛 | 数値(value) | 画面上の位置(position) |
| 線形 |  |  |
| 対数 |  |  |
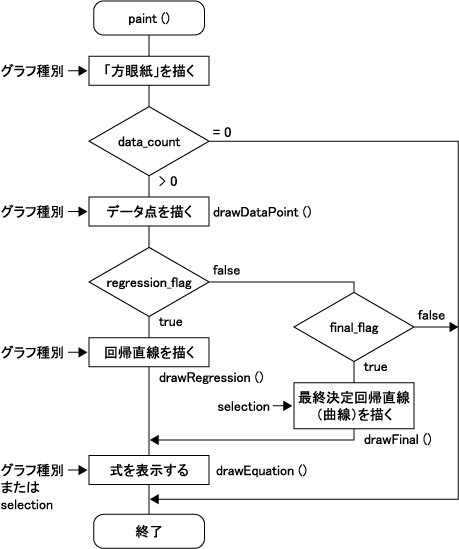
プログラムの主要部分paint()の動作
paint()は、起動時の他、ボタンのクリックやマウスの操作の都度、repaint()によって呼び出され、以下のような動作をします。
アプレットを起動した直後(regression_flag=false、final_flag=false)
- ラジオボタンで選択されたグラフ種別(デフォルトは、[線形→線形])に応じて「方眼紙」を描く。
- データが入力されて、
data_count>0であれば、データ点を赤丸で表示する。(drawDataPoint())。
data_value[i]が生成されるので、それを現在選択しているグラフ種別に応じて、画面上の位置に変換して赤丸を描画する。データ入力が終わり、[回帰直線]ボタンをクリックした後(regression_flag=true、final_flag=false)
- 上記と同じ。
- 上記と同じ。
- 回帰直線を描く(
drawRegression())。 - 回帰直線の式を表示する(
drawEquation())。
data_value[i]を、グラフ種別に応じて画面上の位置(x[i], y[i])の値に変換し、これらから画面上の回帰直線の係数a、bを求めて格納する。同時に、この係数を用いて、ax+bを計算し、画面上に回帰直線を描画する。a、bを式の形に変換し、表示する。適切なグラフ種別を選び、[回帰決定]ボタンをクリックした後(regression_flag=false、final_flag=true)
- 上記と同じ。
- 上記と同じ。
- 回帰直線(グラフ種別によっては曲線)を描く(
drawFinal())。 - 回帰直線(または曲線)の式を表示する(
drawEquation())。
regression_value[i]を、現在選定中のグラフ種別に応じて画面上の位置に変換し、直線(または曲線)を青色で描画する。selectionの値([回帰決定]時のグラフ種別を保持している)に応じて、係数a、bを式の形に変換し、表示する。以上のフローチャートを下図に示します。
プログラム
import java.applet.Applet; import java.awt.*; import java.awt.event.*; import java.awt.geom.Point2D; public class Least extends Applet implements MouseListener,MouseMotionListener,ItemListener,ActionListener{ static final int X0=50,Y0=50; //「方眼紙」の左上座標 static final int SIZE=5; //目盛の最小間隔 int data_count; //入力データ個数 //入力データの画面上のピクセル位置 Point[] data_position=new Point[20]; //入力データの数値 Point2D.Double[] data_value=new Point2D.Double[20]; //回帰曲線の数値 Point2D.Double[] regression_value=new Point2D.Double[100*SIZE+1]; Checkbox radio1,radio2,radio3,radio4; Button button1,button2,button3,button4; boolean regression_flag; //[回帰直線]がクリックされるとtrueになる boolean final_flag; //[回帰決定]がクリックされるとtrueになる double a,b; //回帰直線の係数 int selection; //[回帰決定]時のグラフ種別 // ------------------------ 初期設定 ---------------------------- public void init(){ data_count=0; regression_flag=false; final_flag=false; //マウス関係準備 addMouseMotionListener(this); addMouseListener(this); //チェックボックス関係準備 CheckboxGroup radio=new CheckboxGroup(); add(radio1=new Checkbox("線形→線形",radio,true)); add(radio2=new Checkbox("線形→対数",radio,false)); add(radio3=new Checkbox("対数→線形",radio,false)); add(radio4=new Checkbox("対数→対数",radio,false)); radio1.addItemListener(this); radio2.addItemListener(this); radio3.addItemListener(this); radio4.addItemListener(this); //ボタン関係準備 add(button1=new Button(" 回帰直線 ")); add(button2=new Button(" 回帰決定 ")); add(button3=new Button(" 回帰消去 ")); add(button4=new Button("データ消去")); button1.addActionListener(this); button2.addActionListener(this); button3.addActionListener(this); button4.addActionListener(this); } // ------------------- マウス関係メソッド ----------------------- //マウスを動かすと、対応する数値を表示する public void mouseMoved(MouseEvent me){ Graphics g=getGraphics(); int x=me.getX(); int y=me.getY(); Point position=new Point(x-X0,Y0+100*SIZE-y); //位置を数値に変換する Point2D.Double value=changeToValue(position); g.setColor(Color.yellow); g.fillRect(X0+100*SIZE+10,Y0,140,50); //前の表示を消すのに使用 g.setColor(Color.black); //「方眼紙」の範囲内 if(x>=X0 && x<=X0+100*SIZE && y>=Y0 && y<=Y0+100*SIZE){ g.drawString("X座標= "+ (float)value.x ,X0+100*SIZE+30,Y0+20); g.drawString("Y座標= "+ (float)value.y ,X0+100*SIZE+30,Y0+40); } else g.drawString("範囲外です。",X0+100*SIZE+50,Y0+20); } //使用しないが、記述しておかないとエラーになる public void mouseDragged(MouseEvent me){ } //マウスをクリックするとデータの数値を格納する public void mousePressed(MouseEvent me){ int x=me.getX(); int y=me.getY(); Point position=new Point(x-X0,Y0+100*SIZE-y); //「方眼紙」の範囲内 if(x>=X0 && x<=X0+100*SIZE && y>=Y0 && y<=Y0+100*SIZE){ //位置を数値に変換する data_value[data_count]=changeToValue(position); data_count++; repaint(); } } //使用しないが、記述しておかないとエラーになる public void mouseClicked(MouseEvent me){ } public void mouseEntered(MouseEvent me){ } public void mouseReleased(MouseEvent me){ } public void mouseExited(MouseEvent me){ } // --------------- チェックボックス関係メソッド ----------------- //グラフの種別が変更された public void itemStateChanged(ItemEvent ie){ repaint(); } // ------------------ ボタン関係メソッド ------------------------ //ボタンがクリックされた public void actionPerformed(ActionEvent ae){ if(ae.getSource()==button1){ //回帰直線の描画 regression_flag=true; button1.setBackground(new Color(255,220,150)); final_flag=false; button2.setBackground(new Color(215,215,195)); repaint(); } if(ae.getSource()==button2){ //回帰決定 final_flag=true; button2.setBackground(new Color(255,220,150)); regression_flag=false; button1.setBackground(new Color(215,215,195)); createRegressionValue(); //回帰直線の値を生成し格納する if(radio1.getState()) selection=1; if(radio2.getState()) selection=2; if(radio3.getState()) selection=3; if(radio4.getState()) selection=4; repaint(); } if(ae.getSource()==button3){ //回帰直線(曲線)を消去 regression_flag=false; button1.setBackground(new Color(215,215,195)); final_flag=false; button2.setBackground(new Color(215,215,195)); repaint(); } if(ae.getSource()==button4){ //データを消去 regression_flag=false; button1.setBackground(new Color(215,215,195)); final_flag=false; button2.setBackground(new Color(215,215,195)); data_count=0; for(int i=0;i<20;i++){ data_value[i]=new Point2D.Double(0.0,0.0); } repaint(); } } // ---------------------- 描画、再描画 -------------------------- public void paint(Graphics g){ int i,x,y; //方眼紙」を描く if(radio1.getState()){ //線形→線形 drawLinearHorizontal(); drawLinearVertical(); } if(radio2.getState()){ //線形→対数 drawLinearHorizontal(); drawLogVertical(); } if(radio3.getState()){ //対数→線形 drawLogHorizontal(); drawLinearVertical(); } if(radio4.getState()){ //対数→対数 drawLogHorizontal(); drawLogVertical(); } if(data_count>0) drawDataPoint(); //データ点を描く else return; if(regression_flag) drawRegression(); //回帰直線を描く else if(final_flag) drawFinal(); //最終決定回帰曲線を描く else return; drawEquation(); } // ---------------- 「方眼紙」作成用メソッド -------------------- //線形横軸 private void drawLinearHorizontal(){ int i,d; Graphics g=getGraphics(); for(i=0;i<=50;i++){ d=2*SIZE*i; if(i % 5==0){ g.setColor(Color.gray); g.drawLine(X0+d,Y0,X0+d,Y0+100*SIZE); g.setColor(Color.black); g.drawString(String.valueOf(2*i),X0-5+d,Y0+100*SIZE+24); } else{ g.setColor(Color.lightGray); g.drawLine(X0+d,Y0,X0+d,Y0+100*SIZE); } } } //線形縦軸 private void drawLinearVertical(){ int i,d; Graphics g=getGraphics(); for(i=0;i<=50;i++){ d=2*SIZE*i; if(i % 5==0){ g.setColor(Color.gray); g.drawLine(X0,Y0+100*SIZE-d,X0+100*SIZE,Y0+100*SIZE-d); g.setColor(Color.black); g.drawString(String.valueOf(2*i),X0-30,Y0+100*SIZE+5-d); } else{ g.setColor(Color.lightGray); g.drawLine(X0,Y0+100*SIZE-d,X0+100*SIZE,Y0+100*SIZE-d); } } } //対数横軸 private void drawLogHorizontal(){ int i,d; Graphics g=getGraphics(); for(i=1;i<=10;i++){ d=(int)(50*SIZE*Math.log10(i)); g.setColor(Color.gray); g.drawLine(X0+d,Y0,X0+d,Y0+100*SIZE); g.drawLine(X0+50*SIZE+d,Y0,X0+50*SIZE+d,Y0+100*SIZE); if(i!=7 && i!=9){ g.setColor(Color.black); g.drawString(String.valueOf(i),X0-5+d,Y0+100*SIZE+24); g.drawString(String.valueOf(10*i), X0+50*SIZE-5+d,Y0+100*SIZE+24); } } g.setColor(Color.lightGray); for(i=1;i<=2;i++){ d=(int)(50*SIZE*Math.log10(i+0.5)); g.drawLine(X0+d,Y0,X0+d,Y0+100*SIZE); g.drawLine(X0+50*SIZE+d,Y0,X0+50*SIZE+d,Y0+100*SIZE); } } //対数縦軸 private void drawLogVertical(){ int i,d; Graphics g=getGraphics(); for(i=1;i<=10;i++){ d=(int)(50*SIZE*Math.log10(i)); g.setColor(Color.gray); g.drawLine(X0,Y0+100*SIZE-d,X0+100*SIZE,Y0+100*SIZE-d); g.drawLine(X0,Y0+50*SIZE-d,X0+100*SIZE,Y0+50*SIZE-d); if(i!=7 && i!=9){ g.setColor(Color.black); g.drawString(String.valueOf(i),X0-30,Y0+100*SIZE+5-d); g.drawString(String.valueOf(10*i),X0-30,Y0+50*SIZE+5-d); } } g.setColor(Color.lightGray); for(i=1;i<=2;i++){ d=(int)(250*Math.log10(i+0.5)); g.drawLine(X0,Y0+100*SIZE-d,X0+100*SIZE,Y0+100*SIZE-d); g.drawLine(X0,Y0+50*SIZE-d,X0+100*SIZE,Y0+50*SIZE-d); } } // --------------- 位置←→数値の変換用メソッド ----------------- //数値を位置情報に変換する private Point changeToPosition(Point2D.Double value){ int x=0,y=0; //横軸 if(radio1.getState() || radio2.getState()) //線形 x=(int)(SIZE*value.x+0.5); if(radio3.getState() || radio4.getState()) //対数 x=(int)(50*SIZE*Math.log10(value.x)+0.5); //縦軸 if(radio1.getState() || radio3.getState()) //線形 y=(int)(SIZE*value.y+0.5); if(radio2.getState() || radio4.getState()) //対数 y=(int)(50*SIZE*Math.log10(value.y)+0.5); Point position=new Point(x,y); return position; } //位置情報を数値に変換する private Point2D.Double changeToValue(Point position){ double xx=0.0,yy=0.0; //横軸 if(radio1.getState() || radio2.getState()) //線形 xx=position.x/(float)SIZE; if(radio3.getState() || radio4.getState()) //対数 xx=Math.pow(10,position.x/(float)(50*SIZE)); //縦軸 if(radio1.getState() || radio3.getState()) //線形 yy=position.y/(float)SIZE; if(radio2.getState() || radio4.getState()) //対数 yy=Math.pow(10,position.y/(float)(50*SIZE)); Point2D.Double value=new Point2D.Double(xx,yy); return value; } //最終的な回帰曲線(直線)の値を求める private void createRegressionValue(){ int x,y; Point position; for(int i=0;i<=100*SIZE;i++){ x=i; y=(int)(a*x+b); position=new Point(x,y); regression_value[i]=changeToValue(position); } } // ------- 入力データ点、回帰直線(曲線)描画用メソッド --------- //入力データ点を赤丸で描く private void drawDataPoint( ){ int i=data_count-1; Point position; Graphics g=getGraphics(); g.setColor(Color.red); while(i>=0){ position=changeToPosition(data_value[i]); g.drawOval(X0+position.x-2, (Y0+100*SIZE-position.y)-2, 4, 4); i--; } } //回帰直線の係数a、bを計算して格納し、赤色で直線を描く private void drawRegression(){ Graphics g=getGraphics(); int x,y,x_sum=0,y_sum=0, xx_sum=0,xy_sum=0; for(int i=0;i<data_count;i++){ x=changeToPosition(data_value[i]).x; y=changeToPosition(data_value[i]).y; x_sum+=x; y_sum+=y; xx_sum+=x*x; xy_sum+=x*y; } a=(data_count*xy_sum-x_sum*y_sum)/ (double)(data_count*xx_sum-x_sum*x_sum); b=(y_sum-a*x_sum)/(double)data_count; g.setColor(Color.red); for(x=0;x<=100*SIZE;x++){ y=(int)(a*x+b); if(y>=0 && y<=100*SIZE) g.drawRect(X0+x,Y0+100*SIZE-y,0,0); } } //最終的に決定したな回帰曲線を青色で描く private void drawFinal(){ Graphics g=getGraphics(); int x,y,x_old=0,y_old=0; boolean first_flag=true; //drawLineのための出発点判別に使用 g.setColor(Color.blue); for(int i=0;i<=100*SIZE;i++){ x=changeToPosition(regression_value[i]).x; y=changeToPosition(regression_value[i]).y; if(y<0 || y>100*SIZE || x<0 || x>100*SIZE) { first_flag=true; continue; } if(first_flag){ g.drawRect(X0+x,Y0+100*SIZE-y,0,0); x_old=x; y_old=y; first_flag=false; } else{ g.drawLine(X0+x_old,Y0+100*SIZE-y_old, X0+x,Y0+100*SIZE-y); x_old=x; y_old=y; } } } //回帰直線(曲線)の式を表示する private void drawEquation(){ Graphics g=getGraphics(); g.setColor(Color.yellow); g.fillRect(X0+100*SIZE+10,Y0+100,140,50); //前の表示を消す String string1=" ",string2=" "; double bb=Math.pow(10,(b/(50*SIZE))); double aa=a/(10*SIZE)*Math.log(10); if((regression_flag && radio1.getState()) || (final_flag && selection==1)){ //線形→線形 string1="y="+String.valueOf((float)a)+"*x"; string2="+"+String.valueOf((float)b/SIZE); } if((regression_flag && radio2.getState()) || (final_flag && selection==2)){ //線形→対数 string1="y="+String.valueOf((float)bb); string2="*exp("+String.valueOf((float)aa)+"*x)"; } if((regression_flag && radio3.getState()) || (final_flag && selection==3)){ //対数→線形 string1="y="+String.valueOf((float)a*10*SIZE); string2="*log10 x+"+String.valueOf((float)b/SIZE); } if((regression_flag && radio4.getState()) || (final_flag && selection==4)){ //対数→対数 string1="y="+String.valueOf((float)bb); string2="*pow(x,"+String.valueOf((float)a)+")"; } g.setColor(Color.black); g.drawString(string1,X0+100*SIZE+20,Y0+120); g.drawString(string2,X0+100*SIZE+30,Y0+140); } }
プログラムの使い方
アプレットを実行すると、上方に左から[線形→線形][線形→対数][対数→線形][対数→対数]のラジオボタンが現われます。起動時にはデフォルトで、[線形→線形]が選択されています。下部には、上記ボタンに従って「方眼紙」が表示されます。一般的には、[線形→線形]のグラフでデータを入力するのが良いでしょう。
「方眼紙」上でマウスを移動すると、右上にマウスポインタの座標が表示され、クリックすると、その場所に「赤丸」が表示されます。「赤丸」は、画面上の位置ではなく、グラフ(「方眼紙」)上の数値を示していますので、「方眼紙」の種別を切り替えると、それに対応して、画面上の位置が変わります。
データ入力後に、上方右側の[回帰直線]ボタンをクリックすると、回帰直線が赤い線で表示され、同時に、回帰直線を表す式が右側に表示されます。
グラフの種別を変えても、それぞれのグラフにおける回帰直線と式が表示されます。理論上適切なグラフ種別(指数関数なら[線形→対数]、冪関数なら[対数→対数]のように)を選び、[回帰決定]ボタンをクリックします。すると以後は、グラフの種別を変えても、対応する回帰直線は表示されなくなり、さきほど決定した特定のグラフ上の[回帰直線]が、そのとき表示されているグラフ種別に応じて変換されて青色で表示されます。
[回帰決定]ボタンをクリックする以前であれば、[回帰直線]ボタンをクリックした後でも、データ点を任意の場所に追加でき、その都度、回帰直線が更新されます。ただし、データ点は20個までに制限されていますので、ご注意ください。
なお、[回帰直線]ボタンをクリックしないで、直接[回帰決定]ボタンをクリックすると、正常な表示が行われないことがあります。
プログラムの実行結果
図2の例は、[線形→線形]グラフ上で、本来、指数関数で表わされるべきデータを入力し、[回帰直線]ボタンをクリック後、[線形→対数]グラフに移り、そこで[回帰決定]ボタンをクリックし、再び元の[線形→線形]グラフに戻った状態を示しています。
[回帰決定]ボタンがクリックされたことを示すために、ボタンの色が変わっています。右上の黄色い枠の中には、マウスポインタの座標値(この例では、たまたまマウスポインタがあった位置を示していますので、意味はありません)、回帰曲線の式が表示されています。
まとめ
最小二乗法は、古くから数値計算の代表的な応用として、実用されています。特に、線形最小二乗法は、多元連立方程式の求解で得られるので、多くの参考資料があります。
統計的な分析では、線形最小二乗法の最も簡単な例である、1次式への当てはめ(回帰直線)が多く用いられますが、物理現象を扱う実験の分野では、平方根を含む冪関数、指数関数、対数関数で当てはめるべき現象が多く、無理に多次元多項式に当てはめるのは無意味です。
非線形最小二乗法もありますが、これらはやや難解で、ケースバイケースのアルゴリズムが用いられ、線形最小二乗法のように統一されたアルゴリズムはありません。
本稿で紹介した、グラフ形式を従来の「線形→線形」のみから「線形→対数」、「対数→線形」、「対数→対数」などに広げ、それらの座標位置で線形最小二乗法を応用する方法は、完全ではないものの、物理現象にも比較的実用可能です。
参考資料
この記事は、筆者のウエブサイト「Visual C++ 6.0の易しい使い方(19)-最小二乗法により、測定データに多項式を当てはめる-(ただし、現在はVisual C++ 2005 Express Edition版に改定)」を全面的に改良し、Java言語に書き直して、分かりやすく加筆したものです。
対数目盛を含むグラフでの最小二乗法について書かれている資料には、以下のものがあります。
- 『なるほど回帰分析』 村上雅人 著、海鳴社、2004年3月
- 『図解でわかる回帰分析-複雑な統計データを解き明かす実践的予測の方法』 涌井良幸・涌井貞美 著、日本実業出版社、2002年6月
プログラムに限ると、下記の参考資料がありますが、いずれも単純な線形最小二乗法です。
- 『Javaによるアルゴリズム事典』 奥村晴彦・杉浦方紀・津留和生・首藤一幸・土村展之 著、技術評論社、2003年5月
- 『Javaによるはじめてのアルゴリズム入門』 河西朝雄 著、技術評論社、2001年6月
- 『よくわかる数値計算-アルゴリズムと誤差解析の実際』 佐藤次男・中村理一郎 著、戸川隼人・永坂秀子 監修、日刊工業新聞社、2001年11月
- 『CとJavaで学ぶ数値シミュレーション入門』 峯村吉泰 著、森北出版、1999年4月
- 『理工系のJava』 小国力・三井栄慶 著、朝倉書店、2004年3月















































