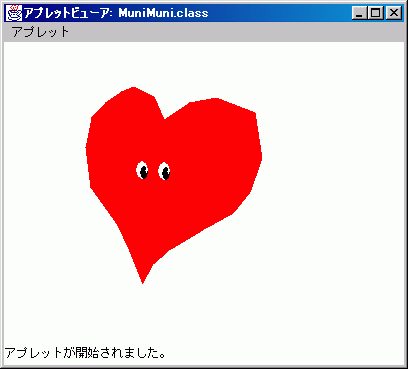
「犬の形をしていたキャラクターがむにむに動いてネコの形に変形! さらに今度はハートの形に変形!」
こんな風に次々に形を変えてくれる、楽しいJavaアプレット「むにむに君」を作ってみましょう。Javaアプレットはホームページに載せることができるので、動きのある楽しいページを演出できます。さらに、この「むにむに君」に新しい形を教えてあげるためのエディタ、「むにえでぃたあ」も作ってみます。このエディタを使うことで、オリジナルの形をむにむに君に教えてあげられるようになります。
モーフィングの赤ちゃん「むにむに君」
「モーフィング」という言葉を聞いたことがあるでしょうか?
コンピュータグラフィックス関係の世界では、異なる2つの形AとBが与えられたときに、Aの形を徐々に変えながらBの形にしてしまう技術をモーフィングと呼びます。「ターミネーター2」で、ターミネーターが液体金属のドロドロした形から人間の形へ変化していくシーンがあったのを覚えている方も多いと思います。これなど、モーフィングを用いた例と言えるでしょう。今回はこのようなモーフィングを用いて、2次元の形が徐々に変化していくJavaアプレットを作成してみます。形が「むにむに」変化していく様子から「むにむに君」と名前をつけてみました:-)。
「むにむに君」作成の流れ
プログラミングを簡単にするために、むにむに君は2次元の平らなキャラクターで、多角形の輪郭を持つ形であることにしましょう。こうすることで、多角形の頂点の位置だけを考えればよくなるので、プログラミングも実際の計算処理も簡単に行えます。
さて、むにむに君は徐々に形を変えていくので、一定時間毎に表示を更新する必要があります。このような処理をするのに必要なのは…そう、スレッドです。今回紹介するアプレットではスレッドを用いてアニメーション表示を行います。まず最初に、むにむに君のプロトタイプの作成にチャレンジします。これは最終的なアプレットの基本となるところだけをプログラミングしてみたシンプルなものです。
プロトタイプがうまく動いたら、いろいろな機能を追加して、むにむに君をもっと楽しいものにしていきます。
最後に、むにむに君に新しい形を教えてあげるための「むにえでぃたあ」の紹介を行います。このエディタを使うことで、オリジナルの形を簡単に追加することができるようになります。むにむに君にかわいくておもしろい形をたくさん教えてあげましょう。
むにむに君のプロトタイプを作ろう
プロトタイプはモーフィングがうまくいくことを試すためのものですから、アルゴリズムを簡単にするために、頂点の数が同じ多角形を2つ用意し、その間だけでモーフィングを行うようにしてみます。具体的には、頂点が10個の星形から、頂点が10個の正10角形へ、徐々に形が変わっていくものを作成します。頂点の数が同じだと、星形の1番目の頂点は正10角形の1番目の頂点へ、星形の2番目の頂点は正10角形の2番目の頂点へ…、という具合に各頂点の移動前と移動後の場所がそれぞれ簡単にわかるので、プログラミングが楽です。
では、それぞれの頂点を始めの場所から終わりの場所まで、徐々に移動させるにはどうすればよいでしょうか? ちょっと数学の話になってしまいますが、始めの場所がP0、終わりの場所がP1で表されるとき、P0とP1をt:1-tに内分する点Qは「Q=(1-t)P0+tP1」という式で表されます(高校時代に勉強したはず!)。このことを使うと、tの値を0から1へ変化させることで、点Qを始めの場所P0から終わりの場所P1へ徐々に移動させることができるようになります(図3)。
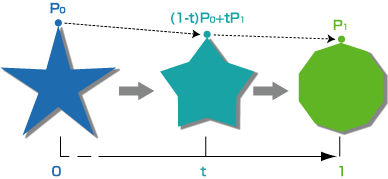
これがむにむに君のアルゴリズムの中で一番大事な部分になります。少し難しい言葉ですが、先ほど記したような式を用いて始めの値と終わりの値から、その間の値を求めることを「線形補間」といいます。後の説明でもまた出てくる言葉なので、ちょっとの間だけ覚えておいてください。この線形補間を、10個の頂点それぞれについて行えば、始めの形と終わりの形から、その間の形を求めることができます。
さて、このようなアルゴリズムを用いて作ったむにむに君のプロトタイプのコードがリスト1です。実行用のhtmlファイルはリスト3のアプレットタグを次のように書き換えます。
<applet code=SimpleMuni.class width=300 height=300 > </applet>
import java.applet.*; import java.awt.*; import java.lang.Math; public class SimpleMuni extends Applet implements Runnable { Thread thread = null; Image bufferImage; //ダブルバッファ用のイメージ Graphics bufferG; int[] x0 = new int[10]; //星形の頂点のx座標配列 int[] y0 = new int[10]; //星形の頂点のy座標配列 int[] x1 = new int[10]; //丸形の頂点のx座標配列 int[] y1 = new int[10]; //丸形の頂点のy座標配列 public void init() { resize(300, 300); bufferImage = createImage(300, 300); bufferG = bufferImage.getGraphics(); bufferImageClear(); //星形と丸形の頂点の座標値計算 for(int i = 0; i < 10; i++) { x0[i] = (int)(150+(40+90*((i+1)%2)) *Math.sin(Math.PI*i*36/180)); y0[i] = (int)(150-(40+90*((i+1)%2)) *Math.cos(Math.PI*i*36/180)); x1[i] = (int)(150+90*Math.sin(Math.PI*i*36/180)); y1[i] = (int)(150-90*Math.cos(Math.PI*i*36/180)); } //スレッドのインスタンス作成と開始 thread = new Thread(this); thread.start(); } public void bufferImageClear() { bufferG.setColor(Color.white); bufferG.fillRect(0, 0, 300, 300); } public void update(Graphics g){ paint(g); } public void paint(Graphics g) { g.drawImage(bufferImage , 0, 0 ,this); } public void run() { try { while (true) { //星形から丸形からへのモーフィング for(int i = 0; i <= 20; i++) { drawMuni((double)i/20); Thread.sleep(50); } Thread.sleep(500); //丸形から星形へのモーフィング for(int i = 20; i >= 0; i--) { drawMuni((double)i/20); Thread.sleep(50); } Thread.sleep(500); } } catch(InterruptedException e){} } public void drawMuni(double t) { bufferImageClear(); Polygon poly = new Polygon(); //中間形状の座標値計算 for(int i = 0; i < 10; i++) poly.addPoint((int)(x0[i]*(1.0-t) + x1[i]*t), (int)(y0[i]*(1.0-t) + y1[i]*t)); //中間形状の描画 bufferG.setColor(Color.blue); bufferG.fillPolygon(poly); repaint(); } }
リスト1のSimpleMuniアプレットを実行すると10個の頂点からなる星形が現れ、その形が徐々に正10角形に変形していきます。正10角形になったあとは、再び星形に戻っていきます。実行結果は下の図1のようになります。実際に動いているものはこちらでご覧いただけます。
さて、それではリスト1を見ていきましょう。プロトタイプ版ですので、頂点の数は10個に固定してしまって、始めの頂点のx座標とy座標をx0[],y0[]に、終わりの頂点のx座標とy座標をx1[],y1[]に格納しています。この間を徐々に移動する頂点のx座標とy座標を、先ほど述べた線形補間の式で計算することで、実際に描画を行う多角形Polygonを作成しています。コードは次のようになっていますね。
Polygon poly = new Polygon(); //中間形状の座標値計算 for(int i = 0; i < 10; i++) poly.addPoint((int)(x0[i]*(1.0-t) + x1[i]*t), (int)(y0[i]*(1.0-t) + y1[i]*t));
「Q=(1-t)P0+tP1」の計算を各頂点のx座標、y座標それぞれに対して行って、新しい頂点の座標値を求めていることがわかるでしょうか。Polygonについてはコラムを参照してください。
スレッドの実際の処理は、run()関数の中で定義されています。Thread.sleep()とdrawMuni()の関数が交互に呼ばれていますね。drawMuni()関数は0から1の値を引数にとって、その値を元に中間形状を表示します。つまり、一定時間停止したら変形と表示を行う、という処理を繰り返すことで、むにむに君のアニメーションを行っているのです。
また、アニメーションがちらつかないように、ダブルバッファを用いていることにも注意しましょう。ダブルバッファの詳細についてはコラムを参照してください。
java.awtパッケージのPolygonクラスは、多角形の情報を格納するためのクラスです。むにむに君のように多角形を描画する必要がある場合には、もってこいのクラスだといえます。addPoint(int x, int y)というメソッドによって、座標値が(x, y)の頂点を多角形に追加することができます。このようにして作成した多角形を表示するには、GraphicsオブジェクトのfillPolygon(Polygon poly)メソッドを使用します。paint()関数の中で描画命令を実行してアニメーションを行うと、画面がちらついてしまったり、描画の途中段階が表示されてしまったりすることがあります。これは、再描画の際に一度画面を背景色で塗りつぶす処理が行われているのと、描画が完了する前に表示が行われてしまうことがある、という2つのことが原因となっています。このような問題を避けるために、まずpublic void update(Graphics g){ paint(g); }
java.lang.Componentクラスのupdate関数をオーバーライドしています)。次に、表示画面と同じ大きさの
Imageオブジェクトを作成して、描画はこのImageオブジェクトに行うようにします。このImageオブジェクトへの描画が終わった段階で、このImageオブジェクトを画面に表示することで、描画の途中段階が表示される問題が解決します。このように、実際に表示される画面と同じサイズのImageを準備して、そちらに描画を行うことをダブルバッファリングと言います。むにむに君を拡張しよう
さて、むにむに君のプロトタイプが動くようになったので、今度はもう少し拡張して、もっと楽しいむにむに君を作ってみましょう。
複数の形を連続変形させよう
せっかく形が変わっていくのに、形が2つだけではつまらないですね。もっとたくさんの形を扱えるようにしましょう。
前回はx0[],y0[],x1[],y1[]という配列を使用していましたが、形が増えるたびにこのような配列を追加していては大変です。そこで、Vectorを使用して複数の形を格納できるようにします。また、新しい形を追加しやすいように、むにむに君の形を表すクラス MuniFigureと、むにむに君のデータを格納するクラスMuniDataを作成しました。
ソースコードの中では、
Vector muniDataVector;
として、むにむに君の形のデータをVectorに格納しています。Vectorについてはコラムを参照して下さい。
MuniMuni:アプレットの本体・
MuniFigure:2つのMuniDataを元に作られる中間形状・
MuniData:形のデータを格納するクラスjava.utilパッケージのVectorクラスは、大きさの変わる配列として扱うことができます。そのため、数が変化したり、はじめに全体の数がわからないようなオブジェクトを格納するのに大変便利です。要素(obj)を追加するには、addElement(Object obj)メソッドを使用します。Vectorはサイズを気にしなくてよいので、このメソッドだけでどんどん要素を追加していくことができます。Vectorに格納されたi番目の要素を取得するには、elementAt(int i)メソッドで取得することができます。Vectorに格納されている要素の数はsize()メソッドで確認できます。頂点数が異なる多角形を扱おう
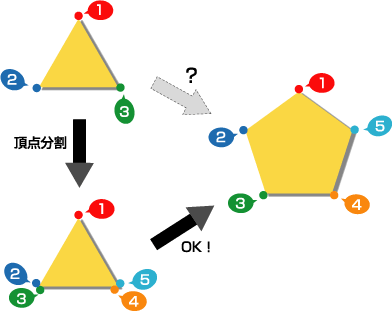
前回は、どちらの形も頂点の数が10個で一緒でした。今度は頂点の数が異なる多角形同士のモーフィングを行ってみましょう。これを厳密に行うとちょっと難しい数式がでてきてしまって大変ですので、モーフィングを始める前に、頂点が少ない方の頂点を分割して、頂点が多い方の頂点と同じ数にしてしまう、という簡単なアルゴリズムで対応してしまうことにします。図2は、3角形と5角形のモーフィングを行う場合の例を示しています。変形を行う前に、3角形を構成する3つの頂点のうちの2つの頂点を分割し、合計5つの頂点にしてしまいます。こうすると、今までのアルゴリズムをそのまま使うことができます。
コードの中では、始まりのMuniDataと終わりのMuniDataを引数とするMuniFigureのコンストラクタで、新しい中間形状を作成しています。
public MuniFigure(MuniData startMuni, MuniData endMuni)
目をつけよう
表情のないキャラクターというのも寂しいものですから、むにむに君に目をつけてみましょう。単なる多角形だけの表現に、ちょっと愛嬌がでてきましたね(図3)。目の動き方は、始めの場所と終わりの場所がわかっているので、他の頂点と同じように計算できます。さすがに目の形をモーフィングするのは難しいので、移動しながら一定時間ごとにまばたきするようにしてみました。
開いた目は、次のようにfillOvalによって楕円を複数描画しています。好みに応じて目の大きさを変えたり、パターンを増やしたりしてもよいですね。
public void drawOpenEyes(Graphics g, Point eye0, Point eye1) { g.setColor(Color.white); g.fillOval(eye0.x, eye0.y, 12,18); g.fillOval(eye1.x, eye1.y, 12,18); g.setColor(Color.black); g.fillOval(eye0.x+4, eye0.y+5, 8,13); g.fillOval(eye1.x+4, eye1.y+5, 8,13); g.setColor(Color.white); g.fillOval(eye0.x+9, eye0.y+7, 3,5); g.fillOval(eye1.x+9, eye1.y+7, 3,5); }

色も変えよう
すべての形が同じ色というのも味気ないものですから、形によって色が変わるようにしてみましょう。今までは頂点の座標を線形補間で求めていましたが、それと同じことを色のR,G,B成分についても行うことで、間の色を求めることができます。実際のコードでは、次のような関数で2つの色の間の色を取得しています。座標値を計算するのと似ていますね。
private Color getColor(int[] c0, int[] c1, double t) { return new Color((int)(c0[0] * (1 - t) + c1[0] * t), (int)(c0[1] * (1 - t) + c1[1] * t), (int)(c0[2] * (1 - t) + c1[2] * t)); }
ここで、c0[0], c0[1], c0[2] はそれぞれ始めの色のRGB成分を、c1[0], c1[1], c1[2] はそれぞれ終わりの色のRGB成分を表しています。
ファイルからデータを読み込もう
プロトタイプ版では、直接コードの中で座標データを計算していましたが、データが変わるたびにコンパイルしていたのでは大変です。そこで、外部ファイルからデータを読み込んで表示するようにしましょう。ファイルアクセスに制限のあるアプレットでも、同じサーバー上のファイルの読み込みは問題なく行えます。今回は、むにむに君アプレットが置かれているディレクトリと同じ場所にある「munidata.txt」というファイルからデータを読み込むことにします。
さて、ファイルからデータを読み込むにはまず、どのような形式でデータがファイルに書き込まれているのかを決める必要があります。具体例として、リスト2のようにデータをファイルに記述しておくことにしました。このファイルを読み込んでむにむに君の形を表示することにします。リスト2は、赤色の3角形と青色の4角形のデータを記述した例です。
まず、「color」という文字列の後に、色のR,G,B成分の値を続けます。次に、「data」という文字列の後に、座標値データがいくつ存在するかを示す値を記します。この値は「頂点の数+2」になります。「+2」になるのは、頂点の座標値に加え、両目の座標値が加わるからです。3角形のデータの場合、「data 5」となっていますね。
この次の行に、最初の頂点のx座標値、y座標値、2番目の頂点のx座標値、y座標値…というように値を続けていきます。ここで、最後の2つ分は目の座標値となります。これで、1つのむにむに君を表すのに必要な情報をすべて記述することができます。あとは、むにむに君の形の数だけこのようなデータを続けて記述していきます。
color 255 0 0 data 5 169 41 81 209 282 209 163 136 184 137 color 0 0 255 data 6 116 59 84 212 254 228 245 77 146 117 194 118
それでは、このファイルを読み込むためのメソッドを作ってみましょう。今回は、上で定義したようなデータファイルを読み込むためのloadData()という関数をリスト3のように作ってみました。この関数は、ファイルからデータを読み込んで、MuniDataのインスタンスを作成し、muniDataVectorに格納していきます。読み込みに成功したらtrueを、失敗したらfalseを返します。
public boolean loadData() { InputStream is = null; MuniData muniData = null; try { is = new URL(getDocumentBase(), DATA_FILE).openStream(); Reader reader = new BufferedReader(new InputStreamReader(is)); StreamTokenizer st = new StreamTokenizer(reader); int token; while((token = st.nextToken()) != StreamTokenizer.TT_EOF) { int x,y; if(token == StreamTokenizer.TT_WORD) { if(st.sval.equals("color")) { muniData = new MuniData(); st.nextToken(); int r = (int)st.nval; st.nextToken(); int g = (int)st.nval; st.nextToken(); int b = (int)st.nval; muniData.setColor(r, g, b); } else if(st.sval.equals("data")) { st.nextToken(); int point_num = (int)st.nval; for(int i = 0; i < point_num; i++) { st.nextToken(); x = (int)st.nval; st.nextToken(); y = (int)st.nval; muniData.addPoint(new Point(x, y)); } muniDataVector.addElement(muniData); } } } is.close(); } catch(Exception e) { return false; } return true; }
アプレットからWeb上のファイルを読み込むには、URLのインスタンスに対してopenStream()メソッドを呼び出し、入力ストリームを取得します。
具体的には、
InputStream is
= new URL(getDocmentBase(), "munidata.txt").openStream();
とすることで、アプレットと同じディレクトリに存在する「munidata.txt」というファイルの入力ストリームを取得できます。
さて、それでは入力ストリームとは何でしょう? この説明を詳しく書くと、とても長くなってしまうので、極めて単純に、「読み込んだデータの流れのこと」だと思ってください。このデータの流れに対して、いろいろな処理を行い、そのデータの中に含まれる文字列や数値を読み込むわけです。リスト3では、空白によって区切られたデータを効率よく読み込むことができるStreamTokenizerを使用して入力ストリームから文字列と数値を読み込んでいます。
StreamTokenizerに対してnextToken()を呼び出すと、入力ストリームから次のデータを取り出し、取り出したデータがどのような型であるかを示す値が返されます。読み込んだデータの値は、そのデータが数値の場合はnvalに、文字列の場合はsvalに格納されます。
主なデータ型と、nextToken()の戻り値は次のようになります。
| データが単語の場合 | StreamTokenizer.TT_WORD |
| データが数値の場合 | StreamTokenizer.TT_NUMBER |
| データがファイルの終わりである場合 | StreamTokenizer.TT_EOF |
リスト3では、この値がファイルの終わりになるまでデータの読み込みを行い、読み込んだ単語が「color」か「data」かに応じて、その後に読み込む数値データの処理を切り替えています。
むにむに君の完成
完成したむにむ君のソースコードはちょっと長くなってしまったので、ここにすべて載せることはできません。詳しくはソースコードを参照してください。
完成したむにむに君は次のようになります。実際に動いているものはこちらでご覧いただけます。

「むにえでぃたあ」を作ろう
今まで、むにむに君の形を新しく追加する場合は、手作業で数値を入力する必要がありましたが、これではあまりにも大変です。JavaではGUIを構築することが比較的簡単にできるので、インタラクティブに形を入力できるエディタを作ってみましょう。むにむに君の形を編集するものなので「むにえでぃたあ」と名づけてみました。
さて、ここで注意しなければならないのは、形のデータをファイルに保存しなければならない、ということです。セキュリティの問題から、一般にJavaのアプレットからハードディスクに直接ファイルを保存することはできません。そこで、ディスクへのアクセス制限のないアプリケーションとして「むにえでぃたあ」を作成してみました。
むにえでぃたあの紹介
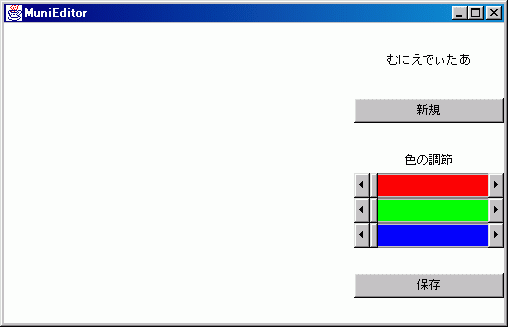
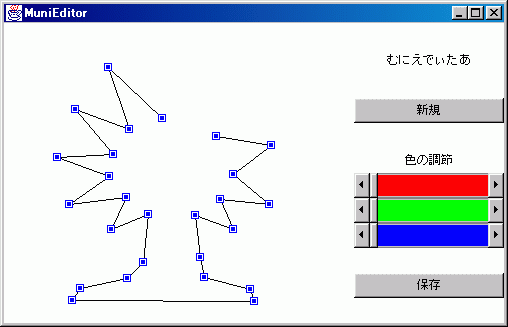
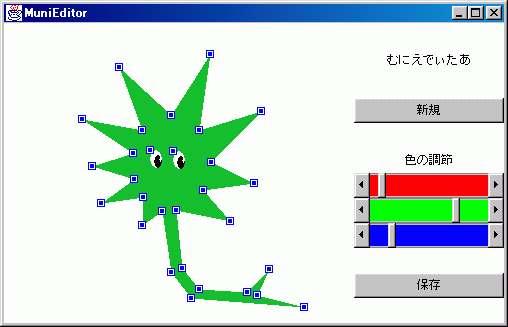
実際に作成してみた「むにえでぃたあ」について紹介します。むにえでぃたあを起動すると図5-1のようなウィンドウが現れます。2つのボタンと、色を調節するためのスライダーのみ、というシンプルなレイアウトです。形の作成と修正はマウスのクリックとドラッグで行います。
むにむに君の新しい形の作成から保存までは次のようなステップで行います。
- おおまかな輪郭線の作成
- 色の決定と輪郭線の微調整
- データの保存
記事上部のリンクから「むにえでぃたあ」のソースコードをダウンロードしてください。コンパイル後、コマンドプロンプトで「java MuniEditor」と入力して実行できます。

さらなる発展(まとめ)
これまでにモーフィングの赤ちゃん「むにむに君」と、そのむにむに君に新しい形を教えてあげるための「むにえでぃたあ」を作ってみました。普段聞き慣れない「モーフィング」のプログラムでしたが、いかがでしたでしょうか? 本稿で紹介した範囲でも、ある程度のものができたと思っていますが、まだまだ工夫次第で独自の楽しいむにむに君が作れそうですね。以下に、さらなる発展のためのヒントを記してみますので、興味のある方はチャレンジしてみてください。
「むにむに君」
- 変形の順番をランダムにする
- 目に動きをつける
- むにむに君に口をつける
- 登録されているむにむに君の形を一覧表示する
「むにえでぃたあ」
- 後から頂点の追加や削除を行なえるようにする
- CGIと連携して、ホームページから形を登録できるようにする















































