Visual C++のC++17対応
並列アルゴリズム:parallel algoritmsはC++17で標準C++に組み入れられました。4年ほど前、parallel algorithmsのMicrosoft実装:ParallelSTLを紹介しました。これがVisual C++で公式サポートされるんじゃないかと期待していたけど、Visual C++ 2017リリース時には入ってなくてがっかりしたんですよね。
で、今年5月のVisual Studio 2017 updateでサポートしたとの情報を耳にして早速更新かけたところ、Visual Studioのバージョンは15.7.x、Visual C++はMSCバージョン19.14にupdateされました。
Visual C++開発チームのblogによると、Visual C++は今回のupdateでC++17対応がおおむね完了したようです。これまでg++、clangに後れを取っていたのがようやく追いついて喜ばしい限り。C++17はコンパイラのコマンドライン・オプションおよびプロジェクト・プロパティに-std:c++17もしくは-std:c++latestの指定をお忘れなく。デフォルトではC++14(-std:c++14)扱いらしいです。

parallel algorithmsおためし
parallel algorithmsによる並列化の効果を確認すべく、そこそこの計算時間を要する処理:与えた自然数が素数か否かを判定するclass prime_judgeを用意しました。
#pragma once
#include <algorithm>
#include <vector>
#include <stdexcept>
class prime_judge {
private:
std::vector<int> primes_;
public:
prime_judge(int N) {
primes_.push_back(2);
// 奇数 3, 5, 7 ... に対し
for ( int n = 3; n <= N; n += 2 ) {
// primes_の中に n を割り切る数がなければ
if ( std::none_of(primes_.begin(), primes_.end(),
[n](int p) { return n%p == 0;}) ) {
// nは素数だからprimes_に追加する
primes_.push_back(n);
}
}
}
// nが素数ならtrueを返す
bool operator()(int n) const {
if ( n > primes_.back()*primes_.back() ) {
throw std::domain_error("too big to determine.");
}
if ( n < 2 ) return false;
return binary_search(primes_.begin(), primes_.end(), n)
|| std::none_of(primes_.begin(), primes_.end(),
[n](int p) { return n%p == 0;});
}
};
コンストラクタに与えたNにより、Nより小さな素数を昇順に並べた素数表を作っておきます。int nが素数ならtrueを返すメンバ関数:bool operator()(int n) constでは、nが素数表に含まれていればtrue、さもなくばnを割り切る素数が素数表内に見つからなければtrueを返します。この方法で、コンストラクタに与えたNに対しN*N未満のnについて素数か否かを判定できます。
prime_judgeとstd::count_ifを使って10万以下の素数がいくつあるか勘定してみました。
#include "prime_judge.h"
#include <iostream>
#include <numeric>
#include <algorithm>
template<typename Iterator>
size_t count_seq(Iterator first, Iterator last, const prime_judge& judge) {
return std::count_if(first, last, judge);
}
int main() {
using namespace std;
prime_judge judge(1000);
vector<int> data(100000);
iota(data.begin(), data.end(), 1); // data を 1, 2 ... 99999 で埋める
size_t count = count_seq(data.begin(), data.end(), judge);
cout << count << " primes found.\n";
}
9592個の素数を見つけましたよ。
それではこいつを並列化します。所要時間をマイクロ秒単位で計測する関数を用意し、自前でスレッド分割するもの、microsoft PPL(Parallel Patterns Library)での実装、そしてC++17 parallel algorithmsによる実装の3本でそれぞれの所要時間をシングルスレッドの順次実行版と比べたスピードアップ率を比べます。
#pragma once
#include <chrono>
template<typename Function>
long long measure(Function fun, int repeat =1) {
using namespace std::chrono;
auto start = high_resolution_clock::now();
while ( repeat-- ) fun();
auto stop = high_resolution_clock::now();
return duration_cast<microseconds>(stop - start).count();
}
#include "prime_judge.h"
#include "measure.h"
#include <iostream>
#include <iomanip>
#include <numeric>
#include <algorithm>
/*
* 順次処理
*/
template<typename Iterator>
size_t count_seq(Iterator first, Iterator last, const prime_judge& judge) {
return std::count_if(first, last, judge);
}
/*
* 自前でスレッド分割
*/
#include <thread>
#include <future>
#include <iterator>
template<typename Iterator>
size_t count_par_byhand(Iterator first, Iterator last, const prime_judge& judge) {
// 物理的に並行動作可能なスレッド数
unsigned int num_threads = std::thread::hardware_concurrency();
// 1つのスレッドが受け持つtask数
size_t step = std::distance(first, last) / num_threads;
std::vector<std::future<size_t>> futures(num_threads);
auto count_prime = [&](Iterator f, Iterator l) -> size_t {
return std::count_if(f, l, judge);
};
Iterator tfirst = first;
Iterator tlast;
for ( unsigned int i = 0; i < num_threads; ++i ) {
tlast = ( i+1 == num_threads ) ? last : std::next(tfirst, step);
futures[i] = std::async(count_prime, tfirst, tlast); // スレッド起動
tfirst = tlast;
}
// 各スレッドで求めた数を積算する
size_t count = 0;
for ( auto& fut : futures ) {
count += fut.get();
}
return count;
}
/*
* Parallel Patterns Library
*/
#include <ppl.h>
#include <atomic>
template<typename Iterator>
size_t count_par_ppl(Iterator first, Iterator last, const prime_judge& judge) {
std::atomic<size_t> count = 0;
concurrency::parallel_for_each(first, last,
[&](int n) { // nが素数ならcount+1
if ( judge(n) ) {
++count;
}
});
return count;
}
/*
* C++17 parallel algorithms
*/
#include <execution>
template<typename Iterator>
size_t count_par_cpp17(Iterator first, Iterator last, const prime_judge& judge) {
return count_if(std::execution::par, first, last, judge);
}
/*--------------------------------------------------*/
void run() {
using namespace std;
prime_judge judge(1000);
vector<int> data(100000);
iota(data.begin(), data.end(), 1);
size_t count;
long long par_dur;
long long seq_dur;
auto percent_change = [](long long o, long long n) { return (o-n)*100/n; };
cout << "sequential: ";
seq_dur =
measure([&]() {
count = count_seq(data.begin(), data.end(), judge);
});
cout << count << " primes found in " << seq_dur << "[us]\n";
cout << "parallelism by hand: ";
par_dur = measure([&]() {
count = count_par_byhand(data.begin(), data.end(), judge);
});
cout << count << " primes found in " << par_dur << "[us] "
<< setw(3) << percent_change(seq_dur, par_dur) << "%\n";
cout << "Parallel Patterns Lib.: ";
par_dur = measure([&]() {
count = count_par_ppl(data.begin(), data.end(), judge);
});
cout << count << " primes found in " << par_dur << "[us] "
<< setw(3) << percent_change(seq_dur, par_dur) << "%\n";
cout << "c++17 parallel algo.: ";
par_dur = measure([&]() {
count = count_par_cpp17(data.begin(), data.end(), judge);
});
cout << count << " primes found in " << par_dur << "[us] "
<< setw(3) << percent_change(seq_dur, par_dur) << "%\n";
cout << endl;
}
int main() {
run(); run(); run(); run(); run();
run(); run(); run(); run(); run();
}
自前でスレッド分割版:std::thread::hardware_concurrency()が返すハードウェアで並行動作可能な数、要するに論理コア数と同数のスレッドを起こし、10万のタスクを均等に切り分けて各スレッドに与え、それぞれの結果を拾って集計しています。async/future使って楽してますが、それでもそこそこメンド臭い実装です。
PPL版ではconcurrency::parallel_for_each()を使いました。複数のスレッドが1つの領域を同時にアクセスすることによって起こるdeta-raceを避けるべく、数の積み上げにatomic<int>を利用しています。自前でスレッド分割するよりずいぶん楽ではありますが、PPLはparallel_count_if()なんて気の利いた関数を持ち合わせていないので、こんな実装となりました。
parallel algoritms版だとあっけないほど簡単、ヘッダ:<execution>に定義された実行ポリシー:std::execution::parをcount_if()の第一引数に与えるだけ。
こんな実行結果が得られました。
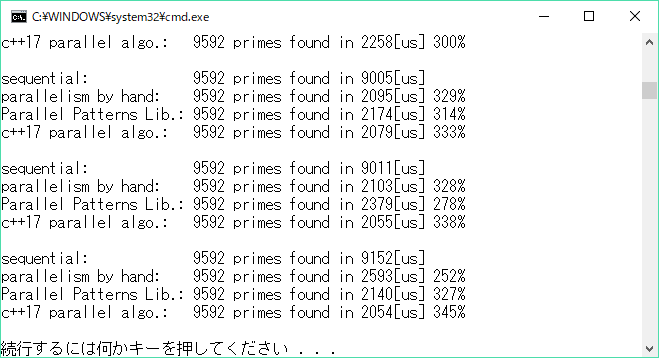
論理コア8個のi7での結果です。並列化したものは、どれも順次実行に比べ約3倍のスピードアップ、parallel algorithmsのお手軽さが光ってますね♪













































