はじめに
三次元グラフは、z=f(x,y)で与えられる関数を分かりやすく表示できるので、多くの科学的論文や資料で使用されます。三次元グラフを描く既製ソフトは数多くありますが、自分でも作れるように、その仕組みを紹介します。三次元座標上の点を、二次元座標上の点に変換する基本が含まれていますので、グラフ作成に限らず、三次元CGの基礎にもなります。
対象読者
数学的な関数や実験結果などを三次元グラフで表示して、論文や資料のアピール度を高めたい人。三次元CGの作成に関心のある人。
必要な環境
J2SE 5.0を使っていますが、それより古いバージョンでも大丈夫です。
三次元グラフの作り方
三次元座標からパソコン画面上の二次元座標への変換
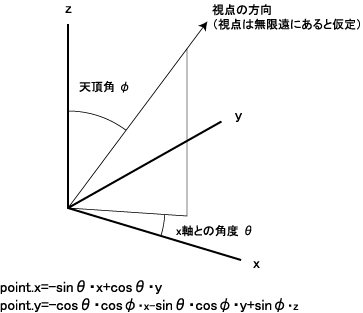
図1に示すように、元になる三次元座標を、変数xとyを水平の平面にとり、関数値zを垂直に選ぶものとします。x軸を水平に、y軸を垂直に、z軸を手前に来るように配置する方式もありますが、ここでは採用しません。z軸からφの角度を持ち、x軸からθの角度を持つ無限遠の視点(無限遠とすると式が簡単になる)から、この三次元座標(x,y,z)の一点を見た(投影した)場合の二次元表示をpoint.xとpoint.yとすると、図の式で表すことができます。実際には、θをマイナスにして使用することが多く、ここではθ=-40°、φ=60°に設定しています。
座標変換のために、メソッドchangeTo2D(double x, double y, double z)を用います。このメソッドには、パソコン画面上の原点(XZERO,YZERO)への加算と、y軸の符号反転が含まれています。引数は、intで与える場合とdoubleで与える場合の両方があります。
三次元グラフの方式
三次元グラフは広く使われているので、目にする機会が多いと思います。多くはワイヤーフレーム方式と呼ばれるもので、一定間隔で関数値を計算し、それらの点を直線または曲線で結びます。この方式は、関数値の急峻な変化に対しても線が途切れることがなく、計算回数が比較的少なく高速である長所があります。しかし、ワイヤーフレームで表示された部分以外の情報が得られないので、細かい変化を表示できない欠点があります。
一方、十分細かい間隔で関数値を計算し、関数値に応じて色を変化させ、そのままプロットする着色方式があります。これにより、上記のワイヤーフレーム方式の欠点をカバーできますが、関数値に急峻な変化がある場合に着色されない部分が生じる欠点があります(計算間隔を狭くすることで防止できますが、計算回数が多くなり、描画が遅くなります)。
ここでは、両者を併用し、着色方式で三次元グラフを描画した後に、全体の形状や座標値を分かり易くするためにワイヤーフレーム方式で線を引いています。
隠線処理
三次元グラフをパソコン上の二次元画面に表示しようとすると、手前の図形によって隠れる部分が生じます。隠れる部分を描画しないテクニックは隠線処理と呼ばれ、最も一般的な方法は最大最小法です。この方法は、グラフを手前の見える部分から順に描画し、パソコン画面上のy軸(垂直)方向の最大値(下方に向かって)と最小値(上方に向かって最大)を蓄えておき、次に描画するグラフの位置がその最小値より小さい場合は隠れていないので描画し、最小値を更新し、大きい場合は隠れているので、描画しません。一方、描画するグラフの位置がそれまでの最大値よりも大きい場合には、下から見えている(裏側が見えている)ので描画し、最大値を更新します。
最大値と最小値を格納するメモリとして、ymax[x]とymin[x]を用意します。ただし、xはパソコン画面上で使用する水平方向のピクセル数で、SIZEなどの条件を基に決定できます。ymax[x]とymin[x]は垂直方向のピクセル値を格納します。
メッシュのように間隔を置いて描画されるワイヤーフレーム方式の隠線処理は工夫を要します。実際に線が描かれていない部分に対しても隠線処理が必要だからです。したがって、ここでは、線を引かない間隙部分に対しても関数値の計算を行い、ymax[x]とymin[x]の更新を行っています。これにより、ワイヤーフレーム方式の長所である計算回数の節減はできなくなります。
プログラムの構成
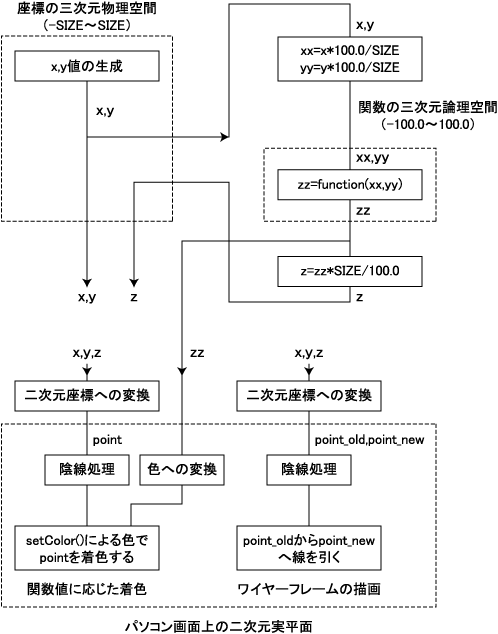
以下のステップからなります。三次元物理空間、三次元論理空間、二次元実平面などの呼び方は、図2を参照してください。
x軸、y軸、z軸を描く
三次元物理空間で、xy平面を水平に配置し、z軸を垂直にとります。各軸の範囲を-SIZEからSIZEまでとして、これを、メソッドchangeTo2Dを使ってパソコン画面上の二次元実平面に変換します。SIZEを外部から与えることにより、グラフの描画サイズを変更できます。
各軸に刻みを入れ、目盛を付ける
目盛は、各軸共に-100~100とし、三次元物理空間上で位置を設定してからメソッドchangeTo2Dで変換し、パソコン上の二次元実平面に描画します。刻みは黒とグレイで交互に入れ、グラフ上のワイヤーフレームの色と対応させ、見やすくします。z軸に関しては、論理空間の関数値(zz)を用いて、メソッドchangeToColorで色に変換して着色します。
メソッドfunction(x,y)で設定した関数関係にしたがって、着色方式でグラフを描画する
図2に示すように、-SIZEからSIZEまで、三次元物理空間上でxとyをスキャンします。ここでは、SIZEとして160を用いていますが、自由に変えることができます。
グラフを描くために関数を計算するには、三次元論理空間に変換する必要があります。グラフの表示範囲を-100.0から100.0と設定してありますので、三次元物理空間のxとyを、それぞれ100.0/SIZE倍して変換します。関数の計算はメソッドfunctionを使用し、結果は、逆にSIZE/100.0倍して、再び三次元物理空間上に戻します。
グラフの着色は、三次元論理空間におけるz軸の値(zzと呼びます)を用います。これは、グラフの目盛(-100から100)の色と一致します。
グラフの着色には、メソッドchangeToColorを用います。changeToColorは、引数入力に対して、青→シアン→緑→黄→赤→マゼンタ→青の順に繰り返して色を変えるように作られています。関数値の絶対値があまり大きくない場合は、引数入力の値に適切な倍率を掛けると見やすくなります(ここでは、1.6倍しています)。
物理空間でのxやyのステップを粗くとる(たとえばステップを1とする)と、実平面への変換結果に隙間ができ、パソコン画面上で表示されない部分が生じる場合がありますので、ここでは、xとyのステップを0.2にしてあります。グラフにさらに急峻な変化部分がある場合は、これでも不十分な場合がありますので、適宜小さくして下さい。
x軸、y軸の目盛に対応させてワイヤーフレーム方式でグラフを描画する
まず、x軸の目盛に対応させて、-100、-80などの目盛が入っている座標に対応するxの位置は黒で、その他はグレイで、y軸と平行に(z軸の無限遠から見た場合)ワイヤーフレームでグラフを描きます。最初、すなわちy=-SIZEの場合は、その時の座標点をpoint_oldとpoint_newの両方に書き込んで、二点間に線を引きます(線ではなく点が描画される)。以後は、前の点をpoint_old、新しく求めた点をpoint_newとして、二点間に線を引きます。xは一回の計算ごとに2を加えて行きますが、実際に線を引くのは、x % (SIZE/10)==0の時だけです。SIZE=160の場合には、xが16増えるごとに線を引きます。線を引かない時は、陰線処理のためのymin[x]とymax[x]だけを必要に応じて更新します。
y軸の目盛に対応させたワイヤーフレームも、x軸の場合と同様にして引きます。
プログラム
import java.awt.*; import java.applet.Applet; public class Graph extends Applet{ final static int THETA=-40,PHI=60; final static int XZERO=90,YZERO=360; final static int SIZE=160; final static double SINT=Math.sin(Math.toRadians(THETA)); final static double SINP=Math.sin(Math.toRadians(PHI)); final static double COST=Math.cos(Math.toRadians(THETA)); final static double COSP=Math.cos(Math.toRadians(PHI)); final int XMAX=XZERO+changeTo2D(SIZE,SIZE,SIZE).x; final int YMAX=YZERO+changeTo2D(SIZE,-SIZE,-SIZE).y; final static String[] scale ={"-100"," -80"," -60"," -40"," -20", " 0"," 20"," 40"," 60"," 80"," 100"}; public void init(){ } public void paint(Graphics g){ Point point,point1,point2,point_old,point_new; int[] ymin=new int[XMAX+1]; int[] ymax=new int[XMAX+1]; // ---------------------- Z-軸の描画 ---------------------- //軸を描く g.setColor(Color.black); point1=changeTo2D(-SIZE,-SIZE,-SIZE); point2=changeTo2D(-SIZE,-SIZE,SIZE); g.drawLine(point1.x,point1.y,point2.x,point2.y); //値に応じて着色する for(int z=-SIZE;z<=SIZE;z++){ //-SIZEを-100に、SIZEを100に対応 g.setColor(changeToColor(z*100.0/SIZE)); point1=changeTo2D(-SIZE,-SIZE-2,z); point2=changeTo2D(-SIZE,-SIZE-10,z); g.drawLine(point1.x,point1.y,point2.x,point2.y); } //目盛を入れる g.setColor(Color.black); for(int i=0;i<11;i++){ point1=changeTo2D(-SIZE,-SIZE,SIZE/5*i-SIZE); point2=changeTo2D(-SIZE,-SIZE-15,SIZE/5*i-SIZE); //刻みを入れる g.drawLine(point1.x,point1.y,point2.x,point2.y); //数字を入れる g.drawString(scale[i],point2.x-30,point2.y+5); //「Z-Axis」と表示 if(i==5) g.drawString("Z-Axis",point2.x-70,point2.y+10); } // ---------------------- X-軸の描画 ---------------------- //軸を描く g.setColor(Color.black); point1=changeTo2D(-SIZE,-SIZE,-SIZE); point2=changeTo2D(SIZE,-SIZE,-SIZE); g.drawLine(point1.x,point1.y,point2.x,point2.y); //目盛を入れる for(int i=0;i<21;i++){ point1=changeTo2D(SIZE/10*i-SIZE,-SIZE,-SIZE); if(i % 2==0){ point2=changeTo2D(SIZE/10*i-SIZE,-SIZE-15,-SIZE); g.setColor(Color.black); //黒で刻みを入れる g.drawLine(point1.x,point1.y,point2.x,point2.y); //数字を入れる g.drawString(scale[i/2],point2.x-30,point2.y+15); //「X-Axis」と表示 if(i==10) g.drawString("X-Axis",point2.x-70,point2.y+30); } else { point2=changeTo2D(SIZE/10*i-SIZE,-SIZE-10,-SIZE); g.setColor(Color.gray); //グレイで刻みを入れる g.drawLine(point1.x,point1.y,point2.x,point2.y); } } // ------ Y-軸の描画(X-軸に準じるのでコメントは省略)----- g.setColor(Color.black); point1=changeTo2D(SIZE,-SIZE,-SIZE); point2=changeTo2D(SIZE,SIZE,-SIZE); g.drawLine(point1.x,point1.y,point2.x,point2.y); for(int i=0;i<21;i++){ point1=changeTo2D(SIZE,SIZE/10*i-SIZE,-SIZE); if(i % 2==0){ point2=changeTo2D(SIZE+15,SIZE/10*i-SIZE,-SIZE); g.setColor(Color.black); g.drawLine(point1.x,point1.y,point2.x,point2.y); g.drawString(scale[i/2],point2.x,point2.y+15); if(i==10) g.drawString("Y-Axis",point2.x+25,point2.y+30); } else{ point2=changeTo2D(SIZE+10,SIZE/10*i-SIZE,-SIZE); g.setColor(Color.gray); g.drawLine(point1.x,point1.y,point2.x,point2.y); } } // ------------------- 関数値に応じて着色 ----------------- //最大最小法による陰線処理のための準備 for(int i=0;i<=XMAX;i++){ ymin[i]=YMAX; ymax[i]=0; } //X軸、Y軸方向を細かくプロットし、着色する for(double x=SIZE;x>=-SIZE;x-=0.2) for(double y=-SIZE;y<=SIZE;y+=0.2){ //座標上の位置を関数の変数値に変換(物理空間→論理空間)) double xx=x*100.0/SIZE; double yy=y*100.0/SIZE; //関数の計算 double zz=function(xx,yy); //関数の計算値を座標上の位置に変換(論理空間→物理空間)) double z=SIZE/100.0*zz; //陰線処理を実施しながら色を変えてプロットする point=changeTo2D(x,y,z); //上に出ているので描画する(表) if(point.y<ymin[point.x]){ ymin[point.x]=point.y; //色は関数の計算値による g.setColor(changeToColor(zz)); g.drawRect(point.x,point.y,1,1); } //下に出ているので描画する(裏) if(point.y>ymax[point.x]){ ymax[point.x]=point.y; g.setColor(Color.gray); g.drawRect(point.x,point.y,1,1); } } // ------------ Xの値をワイヤーフレームで表示 ------------- //最大最小法による陰線処理のための準備 for(int i=0;i<=XMAX;i++){ ymin[i]=YMAX; ymax[i]=0; } point_new=new Point(); for(int x=SIZE;x>=-SIZE;x-=2) for(int y=-SIZE;y<=SIZE;y++){ //座標上の位置を関数の変数値に変換する double xx=x*100.0/SIZE; double yy=y*100.0/SIZE; //関数の計算 double zz=function(xx,yy); //関数の計算結果の値を座標上の位置に変換する double z=SIZE/100.0*zz; //最初の点をpoint_oldに設定 if(y==-SIZE) point_old=changeTo2D(x,y,z); //それ以外は、前の点をpoint_oldにコピー else point_old=point_new; //新しい点を計算する point_new=changeTo2D(x,y,z); //上に出ているので描画する if(point_new.y<ymin[point_new.x]){ ymin[point_new.x]=point_new.y; if(x % (SIZE/10) ==0){ //色を黒に設定 if(x % (SIZE/5) ==0) g.setColor(Color.black); //色をグレイに設定 else g.setColor(Color.gray); g.drawLine(point_old.x,point_old.y, point_new.x,point_new.y); } } //下に出ているので描画する if(point_new.y>ymax[point_new.x]){ ymax[point_new.x]=point_new.y; if(x % (SIZE/10) ==0){ //色を黒に設定 if(x % (SIZE/5) ==0) g.setColor(Color.black); //色を白に設定 else g.setColor(Color.white); g.drawLine(point_old.x,point_old.y, point_new.x,point_new.y); } } } // ----- Yの値をワイヤーフレームで表示(コメント省略)---- for(int i=0;i<=XMAX;i++){ ymin[i]=YMAX; ymax[i]=0; } for(int y=-SIZE;y<=SIZE;y+=2) for(int x=SIZE;x>=-SIZE;x--){ double xx=x*100.0/SIZE; double yy=y*100.0/SIZE; double zz=function(xx,yy); double z=SIZE/100.0*zz; if(x==SIZE) point_old=changeTo2D(x,y,z); else point_old=point_new; point_new=changeTo2D(x,y,z); if(point_new.y<ymin[point_new.x]){ ymin[point_new.x]=point_new.y; if(y % (SIZE/10) ==0){ if(y % (SIZE/5) ==0) g.setColor(Color.black); else g.setColor(Color.gray); g.drawLine(point_old.x,point_old.y, point_new.x,point_new.y); } } if(point_new.y>ymax[point_new.x]){ ymax[point_new.x]=point_new.y; if(y % (SIZE/10) ==0){ if(y % (SIZE/5) ==0) g.setColor(Color.black); else g.setColor(Color.white); g.drawLine(point_old.x,point_old.y, point_new.x,point_new.y); } } } } //関数のメソッド private double function(double x,double y){ return 50*Math.cos(Math.sqrt(x*x+y*y)/10.0); } //数値をカラーに変換するメソッド private Color changeToColor(double z){ int d,r,g,b; z=z*1.6; //補正(256段階の代わりに160段階をフルスケールにする) if(z>=0) d=(int)z % 256; else d=255-(-(int)z % 256); int m=(int)(d/42.667); switch(m){ //青→シアン case 0: r=0; g=6*d; b=255; break; //シアン→緑 case 1: r=0; g=255; b=255-6*(d-43); break; //緑→黄 case 2: r=6*(d-86); g=255; b=0; break; //黄→赤 case 3: r=255; g=255-6*(d-129); b=0; break; //赤→マゼンタ case 4: r=255; g=0; b=6*(d-171); break; //マゼンタ→青 case 5: r=255-6*(d-214); g=0; b=255; break; default: r=0; g=0; b=0; break; } Color color=new Color(r,g,b); return color.brighter(); //明るめにする } //三次元座標をパソコン上の二次元座標に変換するメソッド private Point changeTo2D(double x,double y,double z){ Point point=new Point(); point.x=XZERO+(int)(-SINT*(x+SIZE)+COST*(y+SIZE)+0.5); point.y=YZERO-(int)(-COST*COSP*(x+SIZE) -SINT*COSP*(y+SIZE)+SINP*(z+SIZE)+0.5); return point; } }
いろいろな三次元グラフの描画例
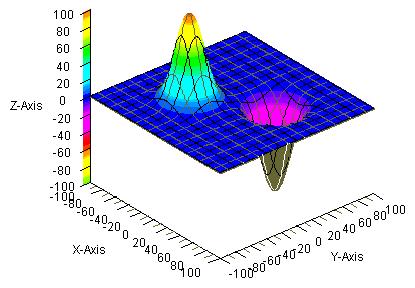
図3は の三次元グラフ、
の三次元グラフ、
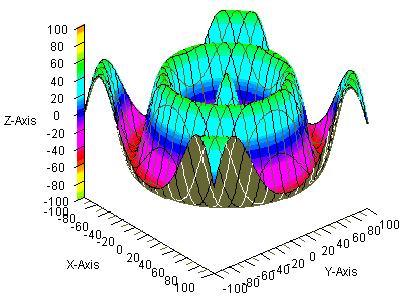
図4は の三次元グラフ、
の三次元グラフ、
図5は の三次元グラフを表した結果です。
の三次元グラフを表した結果です。
いずれの場合も、図の寸法を小さくするために、SIZE=120を使っています。
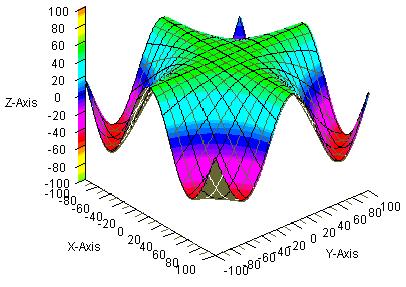
まとめ
三次元グラフを描画するソフトは、有償無償ともに多数ありますが、具体的なプログラムはあまり公表されていません。一方、簡単な方法は多くの参考書にありますが、あまり実用的でありません。ここでは、これらを補い、使いやすい方法を紹介しました。まだ、汎用とはいえませんので、皆さんで、使用目的に応じてカスタマイズしてください。
参考資料
この記事は、筆者のホームページ「Visual C++の易しい使い方(23) ―三次元グラフの陰線処理―」(ただし、現在は Visual C++ 2005 Express Edition 版に改定)を改良してJava言語に書き直し、分かりやすいように加筆したものです。三次元座標を二次元座標に変換する式の導出方法は、「Visual C++の易しい使い方(13) ―三次元グラフィックスの例題としてのFET静特性の表示―」(ただし、現在は Visual C++ 2005 Express Edition 版に改定)の付録に詳しく述べてあります。
三次元グラフの一般的な参考書としては、下記があります。
- 『Javaによるはじめてのアルゴリズム入門』 河西朝雄 著、技術評論社、2001年6月
- 『Javaグラフィックス完全制覇』 芹沢浩 著、技術評論社、2001年12月














































