Curl 3D Gallery技術解説（AD）

Curl 3Dアプリケーションのテクスチャマッピング

第2回

尾松　秀紀[著]

2009/01/29 14:00

ポスト

ダウンロードソースファイル (55.3 KB)

今回はテクスチャマッピングの解説を行います。単純な四角形面にテクスチャを貼る場合はいいのですが、複雑な面にテクスチャを貼る場合は、若干のコツが必要となります。

ポスト

はじめに

　前回に引き続き、9月16日に、住商情報システム株式会社よりプレスリリースされた、「リッチクライアントCurlで開発した3Dアプリケーション「Curl 3D Gallery」の提供を開始」での実装を基にした技術解説の第二弾をお送りします（参照：リッチクライアントCurlで開発した3Dアプリケーション「Curl ３D Gallery」の提供を開始・PDF）。

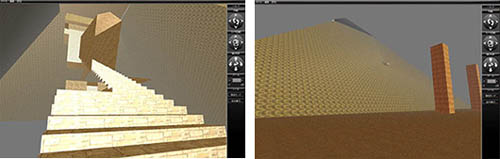
Curl 3D Gallery

前回の記事

Curl 3Dアプリケーション作成の基礎

テクスチャマッピング

　まずは、最も単純なテクスチャマッピングから見ていきましょう。ソースは、「サンプルプログラム：Texture-01」になり、実行結果は次のような画面になります。

　四角形にレンガ模様のイメージを貼り付けたものです。主要部分のソースは次のようになっています。

サンプルプログラム：Texture-01

||-- ① 四角形の頂点座標
let vertices:{Array-of FloatDistance3d} = {new {Array-of FloatDistance3d},
                                              {Distance3d  0in, 10in,  0in} asa FloatDistance3d,
                                              {Distance3d  0in,  0in,  0in} asa FloatDistance3d,
                                              {Distance3d 10in,  0in,  0in} asa FloatDistance3d,
                                              {Distance3d 10in, 10in,  0in} asa FloatDistance3d
                                          }
||-- ② 四角形の各頂点のテクスチャ座標
let texture-coords:{Array-of FloatFraction2d} = {new {Array-of FloatFraction2d},
                                                    {FloatFraction2d 0.0f, 1.0f},
                                                    {FloatFraction2d 0.0f, 0.0f},
                                                    {FloatFraction2d 1.0f, 0.0f},
                                                    {FloatFraction2d 1.0f, 1.0f}
                                                }
||-- ③ 四角形の各頂点の法線ベクトル
let normals:{Array-of FloatDirection3d} = {new {Array-of FloatDirection3d},
                                              {FloatDirection3d  0.0f,  0.0f,  1.0f},
                                              {FloatDirection3d  0.0f,  0.0f,  1.0f},
                                              {FloatDirection3d  0.0f,  0.0f,  1.0f},
                                              {FloatDirection3d  0.0f,  0.0f,  1.0f}
                                          }
||-- ④ 四角形ポリゴンの生成
let polygonset:PolygonSet = {PolygonSet
                                    fill-pattern = {FillPattern.from-url {url "Brick_Rough_Tan.jpg"}}
                                ,   primitive-type = PrimitiveType.polygon
                                ,   vertices = vertices
                                ,   texture-coords = texture-coords
                                ,   normals = normals
                            }
{scene.add-object polygonset}

　四角形ポリゴンの各頂点座標①とその法線ベクトルを指定③し、テクスチャイメージ（④の下線）を指定して、四角形ポリゴンを生成します。

　ここで、②の各頂点のテクスチャ座標とは何なのでしょうか？　ためしに、②を以下の下線部のように変更して、実行してみます。

サンプルプログラム：Texture-02

let texture-coords:{Array-of FloatFraction2d} = {new {Array-of FloatFraction2d},
                                                    {FloatFraction2d 0.0f, 0.5f},
                                                    {FloatFraction2d 0.0f, 0.0f},
                                                    {FloatFraction2d 1.0f, 0.0f},
                                                    {FloatFraction2d 1.0f, 0.5f}
                                                }

　ご覧いただくと分かるように、縦方向が引き伸ばされています。CG（コンピュータグラフィックス）の解説書では、このテクスチャ座標について「uv座標」という表現が用いられています。簡単に言えば、貼り付ける面上の座標系のことです。

　先の例のように、この値を変更することで、張り付くイメージを変形させることもできますし、面が連続している場合に境界部分を違和感なく見せるためにも重要な役割を担っています。同じ面に貼り付けるにも、この値を小さくすればイメージは粗くなり、この値を大きくすればイメージは細かくなります。

イメージを粗くした例

イメージを細かくした例

菱形の場合

　今までは、四角形でしたが、菱形のような図形では、どうでしょう？

　平面座標を菱形となるように変更しただけでは、次のようなイメージとなります。面自体が斜めであれば、これでもいいのですが、面自体が斜めでない場合、テクスチャが傾いてしまっています。

サンプルプログラム：Texture-03

let vertices:{Array-of FloatDistance3d} = {new {Array-of FloatDistance3d},
                                              {Distance3d  5in,  0in,  0in} asa FloatDistance3d,
                                              {Distance3d 10in,  5in,  0in} asa FloatDistance3d,
                                              {Distance3d  5in, 10in,  0in} asa FloatDistance3d,
                                              {Distance3d  0in,  5in,  0in} asa FloatDistance3d
                                          }

　このような場合も、先ほどのテクスチャ座標を正しく設定することで、次のように修正できます。

サンプルプログラム：Texture-04

let texture-coords:{Array-of FloatFraction2d} = {new {Array-of FloatFraction2d},
                                                    {FloatFraction2d 0.5f, 0.0f},
                                                    {FloatFraction2d 1.0f, 0.5f},
                                                    {FloatFraction2d 0.5f, 1.0f},
                                                    {FloatFraction2d 0.0f, 0.5f}
                                                }

　菱形のまま、テクスチャをまっすぐに貼ることができました。

中央にくり抜きのある四角形

　最後に、もっと複雑な場合の例を載せておきます。平面の中央にくり抜きがある例です。

　この例では、ポリゴン座標の指定の方法も今までとは異なっています。今までは各頂点の座標を結ぶ順番に指定していましたが、今回は頂点座標列と面を構成する頂点番号列を指定しています。その際、面を下図のような三角形で構成されるように定義しています。

サンプルプログラム：Texture-05

let vertices:{Array-of FloatDistance3d} = {new {Array-of FloatDistance3d},
                                              {Distance3d  0.0in, 10.0in,  0.0in} asa FloatDistance3d,
                                              {Distance3d  0.0in,  0.0in,  0.0in} asa FloatDistance3d,
                                              {Distance3d 10.0in,  0.0in,  0.0in} asa FloatDistance3d,
                                              {Distance3d 10.0in, 10.0in,  0.0in} asa FloatDistance3d,
                                              {Distance3d  4.0in,  6.0in,  0.0in} asa FloatDistance3d,
                                              {Distance3d  4.0in,  4.0in,  0.0in} asa FloatDistance3d,
                                              {Distance3d  6.0in,  4.0in,  0.0in} asa FloatDistance3d,
                                              {Distance3d  6.0in,  6.0in,  0.0in} asa FloatDistance3d
                                          }

let texture-coords:{Array-of FloatFraction2d} = {new {Array-of FloatFraction2d},
                                                    {FloatFraction2d 0.0f, 2.0f},
                                                    {FloatFraction2d 0.0f, 0.0f},
                                                    {FloatFraction2d 2.0f, 0.0f},
                                                    {FloatFraction2d 2.0f, 2.0f},
                                                    {FloatFraction2d 0.8f, 1.2f},
                                                    {FloatFraction2d 0.8f, 0.8f},
                                                    {FloatFraction2d 1.2f, 0.8f},
                                                    {FloatFraction2d 1.2f, 1.2f}
                                                }

let faces:#{Array-of #{Array-of int}} = {{Array-of #{Array-of int}}.from-size 8, null}
set faces[0] = {new {Array-of int}, 0, 1, 5}
set faces[1] = {new {Array-of int}, 0, 5, 4}
set faces[2] = {new {Array-of int}, 1, 2, 6}
set faces[3] = {new {Array-of int}, 1, 6, 5}
set faces[4] = {new {Array-of int}, 2, 3, 7}
set faces[5] = {new {Array-of int}, 2, 7, 6}
set faces[6] = {new {Array-of int}, 3, 0, 4}
set faces[7] = {new {Array-of int}, 3, 4, 7}

　3次元処理では各面を三角形に分割して扱います。三角形に分割することにより、直線と面の交点座標が面内に存在する点（内包点）なのかの判別を容易にし、曲面を滑らかに表現できます。

おわりに

　「Curl 3D Gallery」でも、SketchUpにより作成された面情報を取り込み時に三角形に分割しており、ウォークスルーでの壁判定や円柱などを滑らかに表現できるようにしています。このようにすることで、複雑な面にテクスチャを貼り付けることも容易にできるようになるわけです。「Curl 3D Gallery」は複雑な処理もあり、理解が難しいところもあると思いますが、今回解説したヒントが紐解く糸口になればと思います。

　次回は、壁判定についてのお話をしようと思います。

この記事は参考になりましたか？