はじめに
前回は一次関数や二次関数のグラフを実際に描いてみました。
今回は、三角関数に関連する図を描いてみます。基本的なD3の利用方法は同じなので、前回までの内容を理解していれば問題ありません。
そこで、今回は基本的な三角関数の復習とともに、動的グラフの更新までを紹介したいと思います。
三角関数の考え方が応用できる領域とは
三角関数は、私たちの身の回りのさまざまな現象に深く関係しています。波の性質を持つものから、一見関係なさそうな分野まで、その関連範囲は幅広いです。
身近な例では、「心電波形などの生体リズム」「地震の振動」「音声波形」などがあります。
これらの波形は、単純な三角関数そのものではありませんが、特定の特徴に着目して分解すると、そこに三角関数が現れてきます。複雑な波形も複数のシンプルな三角関数の波を組み合わせることで表現できるわけです。
また、どうしてここに三角関数が出てくるのだろうという疑問を持つ方もいるかと思います。どのような形で応用する場合でも、三角関数が持つ基本的なイメージを理解することが助けとなるはずです。
三角関数の復習に入る前に、まずは応用される一例を紹介します。
生成AI領域でも活用される三角関数
近年では生成AIの領域でも、「単語」や「文章」の類似度を計算する際に、三角関数の考え方が用いられることがあります。
これは、もちろん「文章」そのものの中に三角関数(円運動や波)の性質が直接含まれているということではありません。膨大な量の過去の文章データを参考に、それぞれの文章や単語が持つ関係性を、仮想上の空間に配置できたとしたら、「位置関係」に変換され、そこで三角関数も使えるという考え方に基づいています。これを「コサイン類似度」と呼びます。
コサイン類似度
AI分野において単語や文章の類似度を測るための「コサイン類似度」という概念があります。これは、図1のように言葉などを空間上の場所に置き換えた時に、それらをベクトル間の角度で測ろうとするものです。
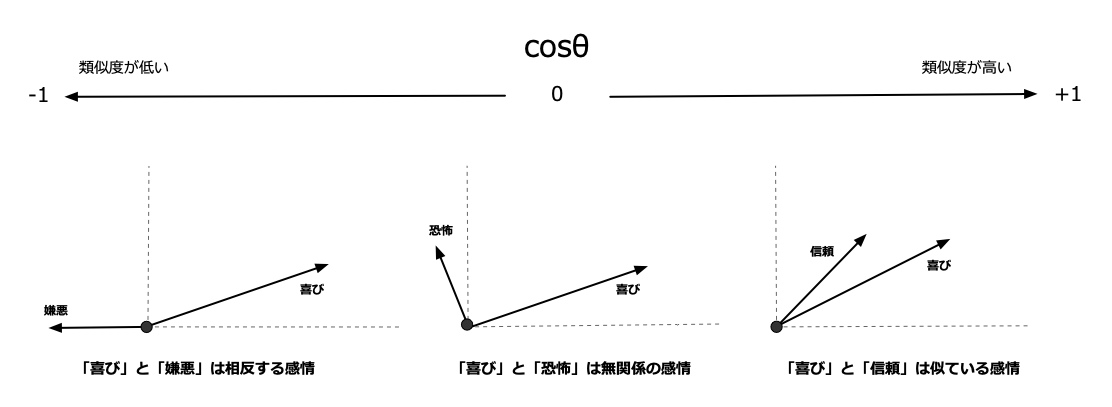
今回はこれらの計算方法についての説明は省略します。ただ、この図を見て、似ているかどうかを判断するために「角度だけを見て、それぞれの位置を見ないのか」と疑問に感じる方もいるでしょう。
実際、2点間の距離で判断する方法(ユークリッド距離)もあります。しかし、距離(ここでは単語の意味の違いと見なしてください)はむしろ考えたくない場合があります。
例えば、「朝のあいさつ」という目的での「おはよう」に似た言葉として、「こんばんは」「よろ」「今朝はいい天気ですね」が候補にあった場合、このケースでは「今朝はいい天気ですね」が一番近いと考えられます。
これは本来は「あいさつ」の言葉ではありませんが、あいさつとしてこのような言葉を使う方も多くいるでしょう。しかし、「あいさつ」という形式として似ているものはどれかになれば、「こんばんは」が望む結果になります。
もし、読者がそれぞれの専門用語の違いについて詳しく分からなくても、「位置(距離)の違い」と「方向の違い」に置き換えて頭の中でイメージできれば判断しやすくなるでしょう。
三角関数が持つ円運動における「位置」と「方向」のイメージは、データ分析においても非常に強力なツールになります。データはしばしば仮想的な空間上に表現され、例えば、今回のケースでは単語や文章の特徴も、数値化され、N次元空間に配置されます。
「N次元空間」と聞くと難しく感じるかもしれませんが、ご安心ください。重要なのはデータ間の類似度が「角度」として捉えることができたという点です。このように、もしデータ間の関係において三角関数の考え方が現れた場合、それらのデータの関係性も、私たちが普段からイメージしやすい「位置」と「方向」の関係の置き換えて捉えられるようになるはずです。















































