はじめに
三角形の形状(正三角形、二等辺三角形、その他の三角形、非三角形)の判定を通して論理的な考え方を解説します。
対象読者
C#の初心者プログラマを想定しています。
必要な環境
Visual Studio .NET 2003が必要です。
プロジェクトの実行
記事上部のリンクからダウンロードしたプロジェクトのテンプレートを適当なところに解凍して、「TriangleCheckTest.sln」をVisual Studio .NETで開いてください。[デバッグ]→[デバッグなしで開始]を選択して実行します。以下の出力が表示されます。
Check(-1, -1, -1) returns その他の三角形, but 非三角形
テストケースの修正
このプロジェクトには、いくつかのテストケースが用意されており、要件を満たさない場合は、エラーメッセージが出力されます。上記の例では、3辺が「-1,-1,-1」の場合に「その他の三角形」と判定されたが、正しくは「非三角形」である、ことを表しています。
辺の長さが0以下の場合には、非三角形となるように直してみましょう。CheckTestクラスのCheckメソッドの「// ここに記述して下さい!」のところに記述します。次のように直してみましょう。
if (d1 <= 0 || d2 <= 0 || d3 <= 0) return Triangle.非三角形;
実行してみましょう。
Check(4...E-324, 4...E-324, 4...E-324) returns その他の三角形,but 正三角形
「...」は、省略を表しています。4E-324は、4×10の-324乗を表し、非常に小さい数字です。上記では、3辺が同じなのに正三角形とならないと言われています。では、Checkメソッドの最初に下記を追加してみましょう。
if (d1 == d2 && d2 == d3) return Triangle.正三角形;
最初と同じようなエラーメッセージになりますね。これは、チェックの順番が正しくないためです。2つのif文を入れ替えて実行しましょう。
Check(4...E-324, 4...E-324, 2) returns その他の三角形, but 非三角形
1辺の長さが2辺の和を超えると三角形ではありません。チェックしてみましょう。3つの長さが順番に並んでいると判定を記述するのが簡単になります。いったん、配列に入れて、並べ替えてみましょう。以下のように直して実行してみましょう。
static Triangle Check(double d1, double d2, double d3) { double[] dd = {d1, d2, d3}; Array.Sort(dd); foreach (double d in dd) if (d <= 0) return Triangle.非三角形; if (dd[0] == dd[2]) return Triangle.正三角形; if (dd[0]+dd[1] <= dd[2]) return Triangle.非三角形; return Triangle.その他の三角形; }
Check(4...E-324, 4...E-324, NaN (非数値)) returns その他の三角形,but 非三角形
辺の長さの型はdoubleです。doubleは、非数値を表すNaNという値を取ることができます。3辺の中に、NaNがあれば、非三角形としてみましょう。3行目を以下のように直し実行します。なお、「d == double.NaN」という判定のしかたは正しくありません。「double.IsNaN」を使うようにしましょう。
foreach (double d in dd) if (d <= 0 || double.IsNaN(d)) return Triangle.非三角形;
Check(4...E-324, 2, 2) returns その他の三角形, but 二等辺三角形
今度は2等辺三角形を判断してみましょう。以下のコードはどこに入れればよいでしょうか?
if (dd[0] == dd[1] || dd[1] == dd[2]) return Triangle.二等辺三角形;
正三角形の判定の直後に入れてみると、
Check(4...E-324, 4...E-324, 2) returns 二等辺三角形, but 非三角形
このように出てしまいます。では、returnの直前に移動してみましょう。
Check(4...E-324, 2, 2) returns 非三角形, but 二等辺三角形
これはどうしたことでしょうか。実は、「4...E-324 + 2 <= 2」はtrueになります。4E-324は非常に小さいので2を足すとコンピュータ上では、2そのものになってしまうのです。どうすればいいのか、よく考えてみて下さい。
if (dd[0] == double.Epsilon && dd[1] == dd[2]) return Triangle.二等辺三角形;
Check(4...E-324, +∞, +∞) returns 二等辺三角形, but 非三角形
doubleは、無限大を表す「+∞」という値を取ることができます。3行目を以下のように直しましょう。
foreach (double d in dd) if (d <= 0 || double.IsNaN(d) || double.IsInfinity(d)) return Triangle.非三角形;
Check(2, 1...E+308, 1...E+308) returns 非三角形, but 二等辺三角形
1...E+308は、非常に大きい数字です。ですが、上記は二等辺三角形と判定しなければいけません。さて、考えはまとまりましたか? dd[1]とdd[2]が等しければ、dd[0]が0を超えている限り、dd[0]+dd[1] > dd[2]となります。従って、以下のように判定すればOKです。
static Triangle Check(double d1, double d2, double d3) { double[] dd = {d1, d2, d3}; Array.Sort(dd); foreach (double d in dd) if (d <= 0 || double.IsNaN(d)|| double.IsInfinity(d)) return Triangle.非三角形; if (dd[0] == dd[2]) return Triangle.正三角形; if (dd[1] == dd[2]) return Triangle.二等辺三角形; if (dd[0]+dd[1] <= dd[2]) return Triangle.非三角形; if (dd[0] == dd[1]) return Triangle.二等辺三角形; return Triangle.その他の三角形; }
Check OK
全テストケース通りました。いかがでしょうか。二等辺三角形の判定、dd[0] == dd[1] || dd[1] == dd[2]を別の行に分けるという発想が必要でしたね。
まとめ
- doubleの取りうる範囲を考慮した判定方法を解説しました。













































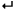 but 正三角形
but 正三角形

